咕咕正在学习高维空间几何， 课堂上老师介绍了超矩形， 它是矩形在高维空间的扩展， 一个 k 维超矩形， 可以用k个正整数$(a_1,\cdots,a_k)$表示，称为它的边长， 而这k个数的乘积，称作体积。比如， 当 k=1时，它是一条直线，体积为$a_1$，我们常称为长度；当k=2时，它是一个长方形， 体积为$a_1\times a_2$，也常称为面积； 当k=3时，它是一个长方体，体积为$a_1\times a_2\times a_3$，以此类推。对于边长分别为$(c_1,\cdots,c_k)$ 与 $(d_1,\cdots,d_k)$的超矩形，只要存在一个$1\le i\le k$ 使得$c_i\neq d_i$，我们就认为这两个超矩形不同。
淘气的咸鱼觉得超矩形实在是太无聊了，决定把它变形一下。他设计了一个长度为k 的十进制数， 这个十进制数中只由0 到9 其中不超过5个数组成（如 023111,12312398，而123456不满足），记为 $b=\overline{b_1b_2\cdots b_k}(0\le b_i\le 9)$，并用这个十进制数对超矩形进行伸缩变换， 使得原本边长为$(a_1,a_2,\cdots ,a_k)$的超矩形对应变成了边长为$(a_1,a_2,\cdots ,a_k)$的超矩形。
为了检验咕咕的学习效果， 咸鱼现在希望咕咕找出所有体积小于等于n的k维超矩形，然后计算它们用给定的b进行伸缩变换后它们的体积的和，对 998244353 取余。
然而可怜的咕咕对这个问题无从下手，便来求助学过 OI 的聪明的你。
输入
输入的第一行包含一个正整数 T，表示数据组数，接下来有 2T 行，每两行代表一组询问。
每组询问的第一行两个正整数 n, k ，n, k 的具体含义见题目描述。
第二行首先一个正整数 q，接下来有 2q 个数字 $r_1,s_1,r_2,s_2,\cdots,r_q,s_q$，它代表了数字b是由连续$s_1$个$r_1$、连续$s_2个r_2、\cdots、连续s_q 个r_q$ 拼接而成的，其中$r_1,r_2,\cdots ,r_q$ 各不相同，且$s_1+s_2+\cdots+s_q=k$。
同一行的相邻两个数字之间有且仅有一个空格，且行首行末均无多余空格。
输出
每行代表一组询问的答案。
对于每组询问，输出一个非负整数，表示答案模 998244353 的结果。
样例

样例输入
1
100 1
1 0 1
样例输出
100
所有超矩形的体积均被变为 1，故答案为找到的超矩形个数，即 100。
样例输入    
1
1000000 1
1 1 1    
样例输出
878323500

所有超矩形的体积均不变，故答案为找到的所有超矩形的体积的和， 为500000500000，取余后为878323500。

样例输入    
4
4 2
1 0 2
4 2
2 0 1 1 1
4 2
2 1 1 0 1
4 2
1 1 2    
样例输出
8
15
15
23
体积为1的超矩形有(1,1)，体积为2的超矩形有(1,2),(2,1)，体积为3的超矩形有(1,3),(3,1)，体积为4的超矩形有(1,4),(2,2),(4,1)。总共有8个。
当 b = 00 时，变换后均变为 (1,1) 的超矩形，故答案为 8。
当 b = 01 时，变换为 (1,1), (1,2), (1,1), (1,3), (1,1), (1,4), (1,2), (1,1)，答案为 15。
当 b = 10 时，变换为 (1,1), (1,1), (2,1), (1,1), (3,1), (1,1), (2,1), (4,1)，答案为 15。
当 b = 11 时，体积不变，答案为 1 × 1 + 2 × 2 + 3 × 2 + 4 × 3 = 23。

样例输入    
2
100 2
2 1 1 0 1
10000 15
5 0 5 1 4 2 3 3 2 4 1    
样例输出
8299
67094893
b 分别等于 10 与 000001111222334。

样例输入    
1
1000000 50000
5 9 10000 8 10000 7 10000 6 10000 5
10000    
样例输出
971676987

数据范围

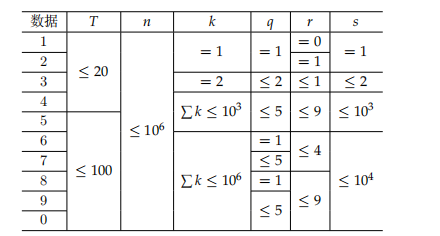
对于所有数据点，T,n,k,q,s均为正整数，$0\le r\le 9$，且 $\sum{q} \le 100$。
其中， $\sum{k}$ 与$\sum{q}$分别表示对同一数据点下的k与q求和。