【题目描述】
小 M 非常不擅长数学。
小 M 在学习数学里的「集合」部分时就被一道题难住了。
题目会给出 n 个集合 A1···n,满足 Ai 里的元素都严格小于 i。
可以通过这些集合构造另外 n 个集合 B1···n,其中 Bi = {i} ∪ (∩k∈AiBk),也就是所
有以 Ai 中元素为下标的 B 集合的公共部分再额外加入一个 i。
小 M 读完题,写下所有的 B 集合之后就不会做了。
但小 M 很好奇这些集合的性质,所以他会询问你 q 次若干个 B 集合的 并. 集. 的大小,
通过了这题他的数学水平就能蒸蒸日上了。
【输入格式】
从文件 upupup.in 中读入数据。
第一行一个整数 n 表示集合个数。
接下来 n 行,每行第一个数 ci 表示第 i 个集合的数的个数,接下来是 ci 个小于 i 的
数,代表 Ai 中的元素。
接下来一行一个整数 q 表示询问组数。
接下来 q 行,每行第一个数 ki 表示当前询问涉及到的集合数量,接下来 ki 个整数
分别表示询问的集合 B 的编号。
【输出格式】
输出到文件 upupup.out 中。
共 q 行,每行一个整数表示对应若干 B 集合的并的大小。
【样例 1 输入】
7 0 1 1 1 1 1 2 2 2 3 0 2 2 6 3 2 2 3 2 3 5 2 4 5【样例 1 输出】
3 3 4【样例 1 解释】
根据题意,有 B2 = {1, 2}, B3 = {1, 3}, B4 = {1, 2, 4}, B5 = {1, 5},那么三个询问得 到的并集分别是 {1, 2, 3}, {1, 3, 5}, {1, 2, 4, 5},大小分别为 3, 3, 4。
【样例 2、3、4】
见 /ex_upupup2.in,/ex_upupup3.in,/ex_upupup4.in 与 /ex_upupup2.out, /ex_upupup3.out,/ex_upupup4.out。
【样例 2、3、4】
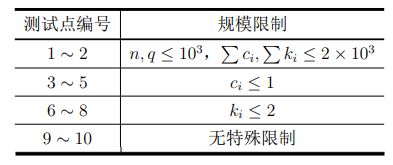
【测试点约束】 对于所有测试点,$1 ≤ n, q ≤ 2 × 10^5,0 ≤ c_i , ∑c_i ≤ 3 × 10^5,0 ≤ k_i , ∑k_i ≤ 2 × 10^6。$ 每个测试点的具体限制见下表: