令 F(n)表示满足下列条件的n+2 个点的无标号混合图的个数:
恰存在一个点没有无向边相邻,恰有一条有向出边,没有有向入边;
恰存在一个点没有无向边相邻,恰有一条有向入边,没有有向出边;
剩下的点中无向边构成一个匹配,每个点恰有一条有向出边,一条有向入边,有向边无自环;
图弱联通。
给定正偶数 n和质数 p,求$F(0) \ mod \ P,F(2) \ mod \ P,...F(n) \ mod \ P$ 。
输入格式
第一行:两个整数n,p 。
输出格式
第一行:(n/2)+1 个数,分别为F(0),F(2),...F(n) 对P 取模后的结果。
样例 1 输入
4 998244353样例 1 输出
1 1 5样例 1 解释
以下为n=4 时5 种不同的图:
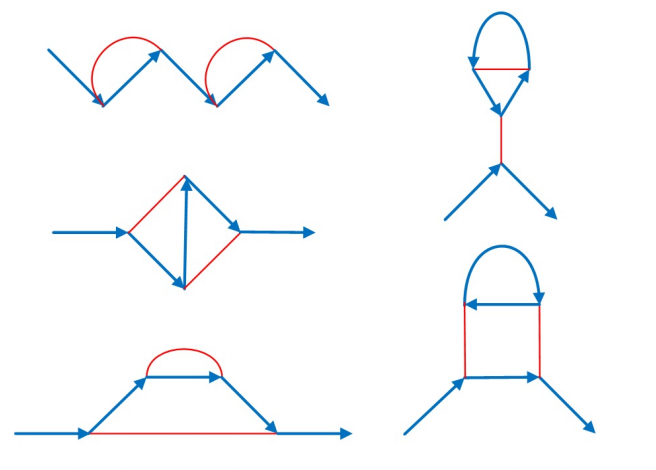
提示
大样例:$F(8)=319,F(114)=741889078(mod \ 998244353) $。
数据范围
对于 100% 的数据:满足$9 * 10^8<=P<=10^9 $,且P为素数。
共有 5个测试点,分别满足n=6,n=50,n=500,n=2000,n=10000 。
