题目描述
我们定义 1 阶斐波那契数列 F1，满足下列递推式：
$F_{1,0} = 1, F_{1,1} = 1$
$F_{1,i} = F_{1,i−1} + F_{1,i−2} (i > 1)$
在此基础上，我们定义 k (k > 1) 阶斐波那契数列$ F_k$。
$F_{k,0} = 1, F_{k,1} = F_{k−1,1} + F_{k,0} $
$F_{k,i} = F_{k−1,i} + F_{k,i−1} + F_{k,i−2} (i > 1)$
给定 k, n，你需要求出 $F_{k,n} $对 469762049 取模的结果。
输入格式
一行两个正整数 k, n。
输出格式
一行一个非负整数表示 $F_{k,n}$ 对 469762049 取模的结果。
样例输入
详见选手文件夹下的 zer o/z ero .in 文件。
样例输出
详见选手文件夹下的 zero/zero .out 文件。
数据规模与约定
本题采用捆绑测试，共 5 个 subtask，你必须通过每个 subtask 中的所有测试点才 能获得该 subtask 的分数。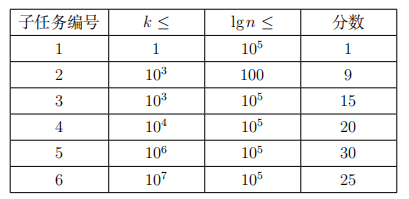

对于全部数据，满足$ 1 ≤ k ≤ 10^7，10 ≤ lg n ≤ 10^5$。
保证 n 在对应数据范围内 .随 .机 .生 .成, 随机方式为每位在 0 ∼ 9 中均匀随机，接着删 去前导 0。
保证每个子任务中只有不超过 5 个测试数据。
Hint
$469762049 = 7 ×2^{26} + 1，$是质数，原根为 3，已知 $13845527^2 ≡ 5 (mod 469762049)。$