Description

小 $N$ 在切蛋糕。

蛋糕是正方形的，放在平面直角坐标系上，左下角在 $(0, 0)$，右上角在 $(S, S)$。

小 N 邀请了 $n$ 个人来提出切蛋糕的建议。每个人都认为应该切恰好两刀，第 $i$ 个人觉得第一刀切在 $(X_{i,1}, Y_{i,1})$ 和 $(X_{i,2}, Y_{i,2})$ 的连线上，第二刀切在 $(X_{i,3}, Y_{i,3})$ 和 $(X_{i,4}, Y_{i,4})$ 的连线上，两条线段之间的区域（包括线段本身）就是他的提案。 保证 $(X_{i,j} , Y_{i,j})$ 一定在蛋糕的边界上，并且保证这两条线段不交叉（但是可能 有共同端点或重合）。 第 $i$ 个人还有一个权值 $c_i$ 。 小 N 需要选出若干个人，使得他们的提案两两交非空，并且最大化权值之和。

注意即使只有一个共同点也认为是交非空。

以下是两个合法方案：

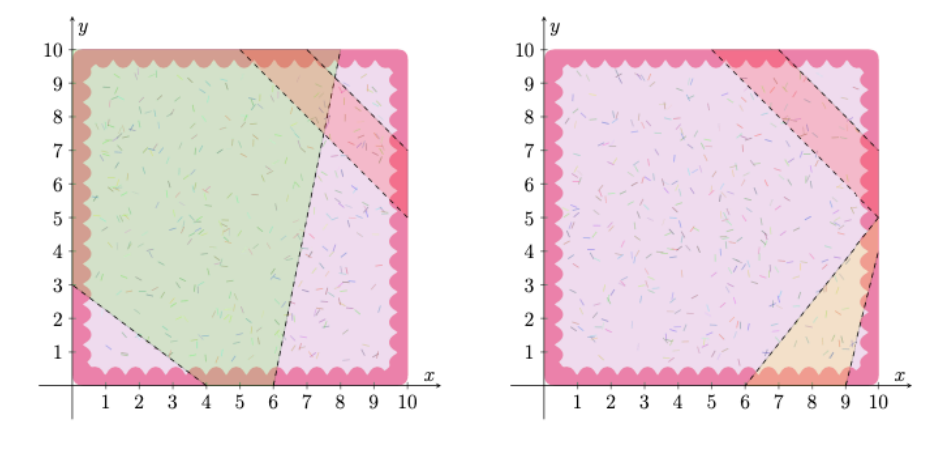
Input Format

第一行一个正整数 $T$ ，表示数据组数。每组数据的输入格式如下：

第一行两个正整数 $S, n$。

接下来 $n$ 行，每行 $9$ 个非负整数 $c_i, X_{i,1}, Y_{i,1}, X_{i,2}, Y_{i,2}, X_{i,3}, Y_{i,3}, X_{i,4}, Y_{i,4}$。

Output Format

对于每组数据，输出一行一个非负整数，表示答案。

Sample #1 Input

3
10 3
20 0 4 10 4 0 6 10 6
30 0 8 10 8 0 9 10 9
40 2 0 2 10 5 0 5 10
4 3
10 0 1 1 0 0 2 2 0
20 0 2 2 4 0 3 1 4
30 2 0 2 4 3 0 3 4
4 4
10 0 1 1 0 0 2 2 0
20 4 2 2 4 4 3 3 4
30 0 2 2 4 0 3 1 4
40 4 1 3 0 4 2 2 0

Sample #1 Output

70
60
60

Sample #1 Explanation

从左到右依次是三组数据的图。

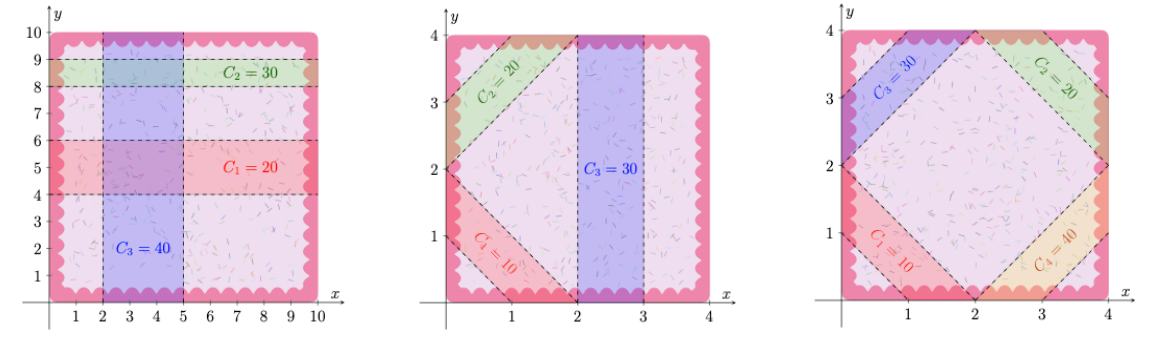
Sample #2 #3

sample

Constraints

本题采用捆绑测试。

对于所有数据，保证 $\sum n\le 2000, 2\le S\le 10^9, 1\le c_i\le 10^6, 0\le X_{i,j}, Y_{i,j}\le S$。

Subtask 1 (20 points) ：$n\le 20$。

Subtask 2 (20 points) ：$X_{i,1} = X_{i,2}, X_{i,3} = X_{i,4}, Y_{i,1} = Y_{i,2}, Y_{i,3} = Y_{i,4}$。

Subtask 3 (35 points) ：$\sum n\le 400$。

Subtask 4 (25 points) ：无特殊限制。