一个形状是凸多边形的奶酪，上面有一些辣椒（对应为图上的一个点），你可以选两个不相邻的顶点将奶酪切下一块，使得这一块中间和边上都没有辣椒。求能切下的最大面积。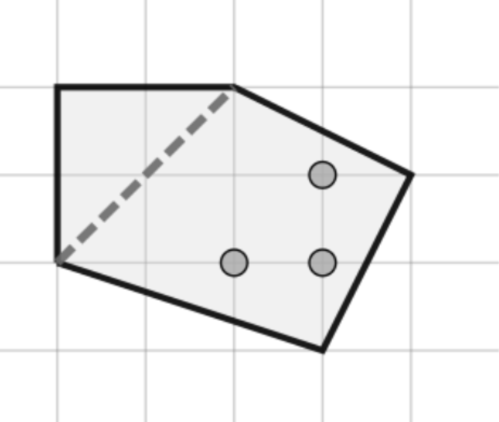

图形对应第一个样例
输入：
第一行一个整数N，表示多边形奶酪顶点的个数。
接下来N个坐标，依次表示每个顶点。
接下来一个数M，表示有M个辣椒。
接下来M个坐标，表示辣椒的位置。
多边形的坐标按逆时针顺序给出，任意两条边都不平行。
所有辣椒的坐标都不相同，且都在多边形内部（也不会在多边形边上）
输出：
一行一个整数，表示切下来的最大面积的两倍（两倍面积总是整数）
无解输出0
SCORING
12％ 4<=N<=300,1<=M<=300
39％ 4<=N<=3000,1<=M<=3000
49％ 4<=N<=300000,1<=M<=300000
所有数据坐标属于［－10^9,10^9］
样例：

输入：
5
0 1
3 0
4 2
2 3
0 3
3
2 1
3 1
3 2
输出：
4
输入：
6
-3 3
-3 -4
-2 -5
2 -5
3 -4
3 3
7
1 0
0 -1
0 -3
2 0
0 0
0 2
-1 0
输出：
10
输入：
6
0 3
-1 2
-1 -2
0 -3
1 -2
1 2
1
0 0
输出：
4

样例2切点2 到点5
样例3切点1到点3.