题目描述
令 $G$ 为一个有向无环图。若 $G$ 的不同顶点 $c_1,c_2,c_3,\ldots c_n$ 满足有一条从 $c_1$ 到 $c_2$ 的路径,有一条从 $c_2$ 到 $c_3$ 的路径,……还有一条从 $c_{n-1}$ 到 $c_n$ 的路径,则称数组 $C = (c_1,c_2,c_3,\ldots c_n)$ 为一个从 $c_1$ 开始,在 $c_n$ 结束的有序数组。
注意对于 $C$ 中任意的两个相邻的元素 $c_i,c_{i+1}$ 不必有直接连接的边,只需要有一条路径即可。
同时,我们定义有序数组 $C = (c_1,c_2,c_3,\ldots c_n)$ 的长度 $\mathrm{len}(C) = n$。因此,一个有序数组的长度即为其中包含的顶点个数。
注意可以存在一个长度为 $1$,从同一个点开始并结束的有序数组。
并且,我们再定义有序数组 $C = (c_1,c_2,c_3,\ldots c_n)$ 的符号 $\mathrm{sgn}(C) = (-1)^{\mathrm{len}(C)+1}$。
对于 $G$ 中的顶点 $x,y$,我们用 $S_{x,y}$ 表示所有从 $x$ 开始并在 $y$ 结束的有序数组的集合。
最后,我们定义顶点 $x,y$ 之间的矛盾值为 $\mathrm{tns}(x,y) = \sum\limits_{C \in S_{x,y}} \mathrm{sgn}(C)$。
也就是说,顶点 $x,y$ 之间的矛盾值等于所有从 $x$ 开始并在 $y$ 结束的有序数组的符号之和。
给定一个整数 $K$,你需要构造一个最多 $1000$ 个点,$1000$ 条边的有向无环图满足 $\mathrm{tns}(1,N) = K$,其中 $N$ 为顶点个数。
顶点以正整数 $1\ldots N$ 编号。
输入格式
第一行,一个整数 $K$。
输出格式
第一行,两个整数 $N,M$ 表示你构造出的有向无环图的点数与边数。
以下 $M$ 行中,第 $i$ 行包含两个不同的整数 $X_i,Y_i$,表示第 $i$ 条边从 $X_i$ 连向 $Y_i$。每条边应最多出现一次。
并且,你的方案需要满足任意两点的矛盾值的绝对值不超过 $2^{80}$。
若有多解,随意输出一解即可。
样例 #1
样例输入 #1
0样例输出 #1
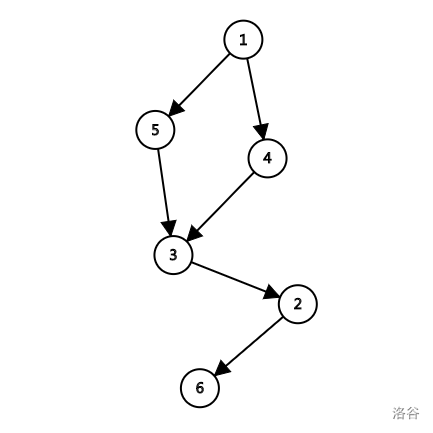
6 6
1 4
1 5
4 3
5 3
3 2
2 6样例 #2
样例输入 #2
1样例输出 #2
1 0样例 #3
样例输入 #3
2样例输出 #3
6 8
1 2
1 3
1 4
1 5
5 4
2 6
3 6
4 6提示
样例 1 解释
构造出的图包含 $6$ 个顶点。从 $1$ 开始在 $6$ 结束的有序数组有:
- $(1, 6)$;
- $(1, 4, 6)$;
- $(1, 5, 6)$;
- $(1, 3, 6)$;
- $(1, 2, 6)$;
- $(1, 4, 3, 6)$;
- $(1, 4, 2, 6)$;
- $(1, 5, 3, 6)$;
- $(1, 5, 2, 6)$;
- $(1, 3, 2, 6)$;
- $(1, 4, 3, 2, 6)$;
- $(1, 5, 3, 2, 6)$。
它们的长度分别为 $1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4$,
所以它们的符号分别为 $-1, 1, 1, 1, 1,-1,-1,-1,-1,-1, 1, 1$。
因此,$1$ 和 $6$ 的矛盾值为 $-1 + 1 + 1 + 1 + 1 - 1 - 1 - 1 - 1 - 1 + 1 + 1 = 0$。
数据范围:
对于 $100\%$ 的数据,$|K| \le 10^{18}$。
各子任务限制见下表:
| 子任务 | 分值 | 限制 |
|---|---|---|
| $0$ | $0$ | 为样例 |
| $1$ | $13$ | $1 \le K < 500$ |
| $2$ | $13$ | $-300 < K \le 1$ |
| $3$ | $18$ | $\lvert K\rvert < 10000$ |
| $4$ | $56$ | - |
