sample

【题目描述】

小明正在参加魔法学校的考试，这次考试涉及两个长度相同的颜色数组 A 和 B。
小明的魔法棒具有独特的功能，能够选择一种颜色，将数组 B 中任意多个相同颜色的元素变成另外一种颜色，这个过程将消耗一次魔法。
然而，这个过程中存在一些特殊颜色对：设一个特殊颜色对是 (u,v,w)，则将颜色 u 变为颜色 v 的操作需要消耗 w 次魔法，保证这些特殊颜色对满足以下条件： 1. 对于任何一个颜色 v，若存在一个特殊颜色对是 (u,v,w)，那么保证数组 B 中所有的颜色为 v 的位置，其在数组 A 中对应的位置颜色也是 v。
2. 给定的所有特殊颜色对 (u,v,w)，则至少存在一个位置 i，使得数组 B 中位置 i 的颜色是 u，而数组 A 中位置 i 的颜色是 v。
小明考试的任务是用最少的魔法次数，将数组 B 的颜色变为与数组 A 完全相同。
你需要帮助小明设计一个算法，计算实现这个目标所需的最少魔法次数。

【输入格式】

输入第一行是两个整数 n, m，表示数组大小与颜色数量。
输入第二行是 n 个整数，第 i 个整数 colorAi (1 ≤ colorAi ≤ m) 表示数组 A 第 i 个元素的颜色。
输入第三行是 n 个整数，第 i 个整数 colorBi (1 ≤ colorBi ≤ m) 表示数组 B 第 i 个元素的颜色。
输入第四行是一个整数 k，表示特殊颜色对的数量。
接下来 k 行，每行三个整数 u, v, w (1 ≤ u, v ≤ m, u≠v, w = 2)，意义如题面所述。

【输出格式】

输出一个整数，表示最少使用魔法的次数。

【样例数据】

样例输入 
5 5
2 4 3 3 2
5 5 4 3 4
2
4 2 2
4 3 2
样例输出
4

【样例解释】

其中一种可行的染色方案为：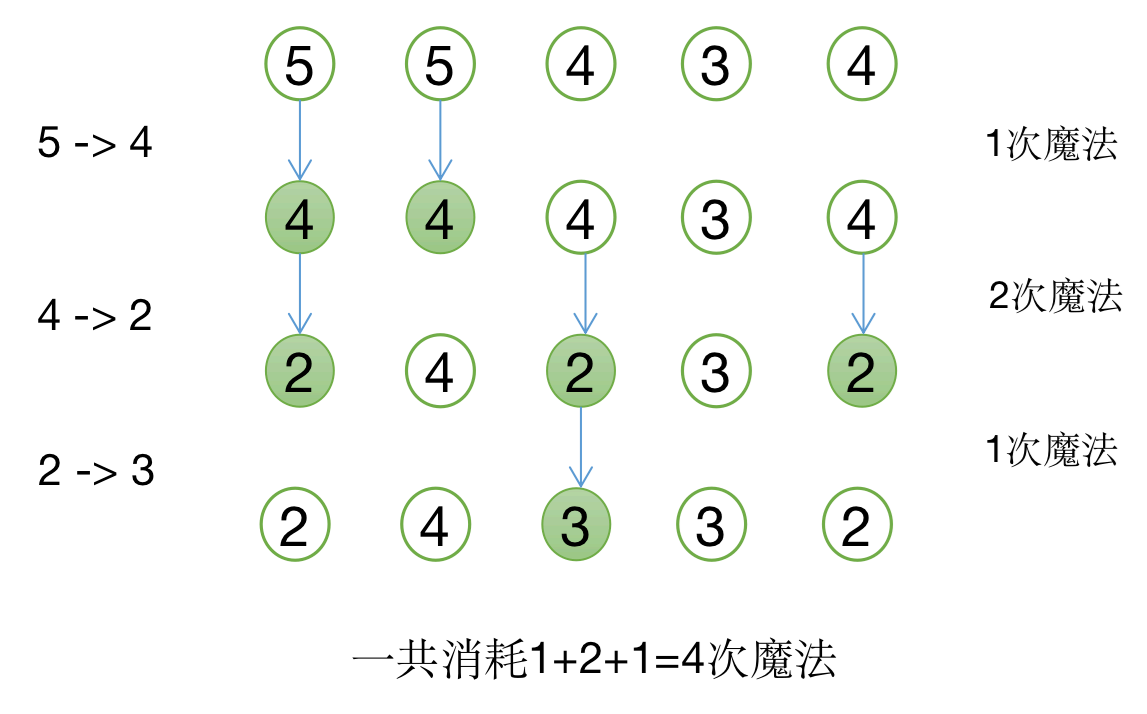

1. 首先将位置 1 和位置 2 的颜色 5 都染色成颜色 4，消耗 1 次魔法。此时 B = [4, 4, 4, 3, 4]
2. 然后将位置 1 和位置 3 以及位置 5 的颜色 4 都染色成 2，因为是特殊颜色对，消耗 2 次魔法。此时B = [2, 4, 2, 3, 2]
3. 最后将位置 3 的颜色 2 染色成颜色 3，消耗一次魔法。此时 B = [2, 4, 3, 3, 2]，与数组 A 颜色完全一致。
故一共消耗了 1+2+1 = 4 次魔法。

【数据范围】

1. 对于 5% 测试点，1 ≤ m ≤ 6。
2. 对于 15% 测试点，1 ≤ m ≤ 12。
3. 对于 25% 测试点，1 ≤ m ≤ 15。
4. 对于 35% 测试点，1 ≤ m ≤ 17。
5. 对于 50% 测试点，1 ≤ m ≤ 20。
6. 对于 65% 测试点，1 ≤ m ≤ 23。
7. 对于另外 15% 的测试点，k = 0。
8. 对于所有的测试点，1 ≤ n ≤ 2 × 10^5, m ≤ 27, 0 ≤ k ≤ 10