题目描述】
原题来自：Waterloo University 2002

北极的某区域共有 n 座村庄，每座村庄的坐标用一对整数 (x,y) 表示。为了加强联系，决定在村庄之间建立通讯网络。通讯工具可以是无线电收发机，也可以是卫星设备。所有的村庄都可以拥有一部无线电收发机， 且所有的无线电收发机型号相同。但卫星设备数量有限，只能给一部分村庄配备卫星设备。

不同型号的无线电收发机有一个不同的参数 d，两座村庄之间的距离如果不超过 d 就可以用该型号的无线电收发机直接通讯，d 值越大的型号价格越贵。拥有卫星设备的两座村庄无论相距多远都可以直接通讯。

现在有 k 台卫星设备，请你编一个程序，计算出应该如何分配这 k 台卫星设备，才能使所拥有的无线电收发机的 d 值最小，并保证每两座村庄之间都可以直接或间接地通讯。

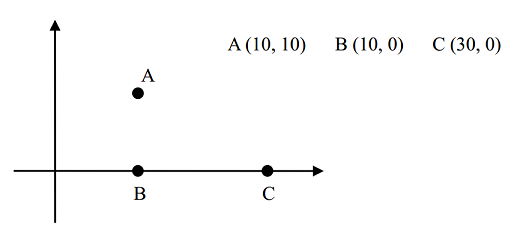
例如，对于下面三座村庄：

其中 |AB|=10,|BC|=20,|AC|=105–√≈22.36
如果没有任何卫星设备或只有 1 台卫星设备 (k=0 或 k=1)，则满足条件的最小的 d=20，因为 A 和 B，B 和 C 可以用无线电直接通讯；而 A 和 C 可以用 B 中转实现间接通讯 (即消息从 A 传到 B，再从 B 传到 C)；

如果有 2 台卫星设备 (k=2)，则可以把这两台设备分别分配给 B 和 C ，这样最小的 d 可取 10，因为 A 和 B 之间可以用无线电直接通讯；B 和 C 之间可以用卫星直接通讯；A 和 C 可以用 B 中转实现间接通讯。

如果有 3 台卫星设备，则 A,B,C 两两之间都可以直接用卫星通讯，最小的 d 可取 0。

【输入】
第一行为由空格隔开的两个整数 n,k;

第 2∼n+1 行，每行两个整数，第 i 行的 xi,yi 表示第 i 座村庄的坐标 (xi,yi)。

【输出】
一个实数，表示最小的 d 值，结果保留 2 位小数。

【输入样例】
3 2
10 10
10 0
30 0
【输出样例】
10.00

对于全部数据，$1≤n≤500,0≤x,y≤10^4,0≤k≤100$。