你正在玩一款休闲益智平台跳跃小游戏。你的目标是让总共M个最初待在最左侧的小红球从左边跳到右边，小红球大小各不相同，按大小从小到大从1到M依次编号。在游戏中，有从左到右N个平台（包括最左和最右，从左到右从1到N编号），其中只有最左边、最右边以及中间的编号为K的平台是牢固的，其余的平台都由浮力支撑，小红球不能在浮力平台上久留。游戏按回合进行，每一回合你可以选择一个小红球向相邻的一个平台跳跃一步，可以向左，也可以向右。但是，这里有些特殊规则需要遵守： 1、选择的小红球必须是在起跳的平台上的小红球中最小的（即编号最小）。 2、小红球完成跳跃后，跳跃的小红球必须是在目标平台上的小红球中最小的。 3、如果该回合小红球跳上了一个浮力平台，下一回合必须马上跳走（不然就会掉下去）。 在遵守以上规则的基础上，你轻松的完成了让所有小红球从最左侧都跳到最右侧的任务，并且你选择了最优的策略，即使用的回合数最少！但是为了证明你没有在吹牛，你现在需要回答一些问题：在某些特定的回合，是编号为几的小红球在跳跃呢？当然，为了方便你的回忆，我们保证问题的答案不会超过30（即最小的30个小红球之一）。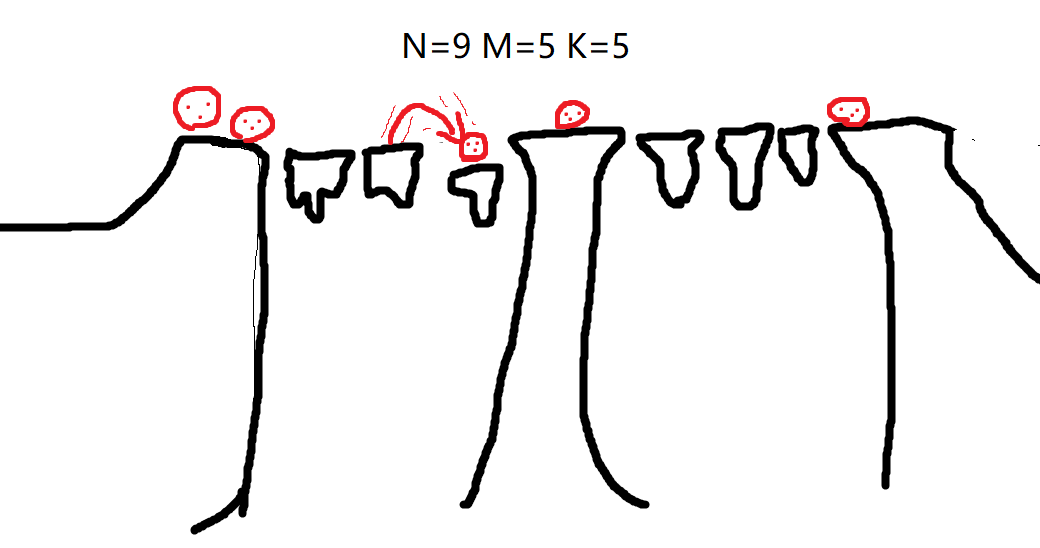

【输入】
第一行三个正整数N，M，K，含义如题面所述。
第二行一个正整数Q，表示问题的个数。
接下来Q行，每行一个正整数Qi表示询问的回合数。
【输出】
输出Q行，每行一个正整数Ansi，表示你对第i个问题给出的回答。
【数据范围】
对30%的数据有 $N\le 10，M\le 10，Q\le 10$
对50%的数据有$N\le 100000000，M\le 10，Q\le 1000$
对所有的数据有：$3\le N\le 100000000，M\le 1000，Q\le 5000 1\lt K\lt N$
Qi小于等于最优策略的回合数，即总是存在合理答案，且答案小于等于30。

【样例输入】
4 2 2
3
1
4
9

【样例输出】
1
2
2