题目描述
小 $\gamma$ 有一张 $n$ 个点 $m$ 条边的有向图,他希望将每个结点染上红、绿、蓝三种颜色之一。为了方便叙述,不妨设点集为 $[1, n] \cap \mathbb N$。
小 $\gamma$ 有两个朋友:我们不妨将他们称为小 $\alpha$ 与小 $\beta$。如果一条有向边是由红色点到绿色点、由绿色点到蓝色点或者由蓝色点到红色点,那么这条边被小 $\alpha$ 喜欢。如果一条有向边的两个顶点颜色一致,那么这条边被小 $\beta$ 喜欢。例如下图中左侧的边是小 $\alpha$ 喜欢的,右侧的边是小 $\beta$ 喜欢的:
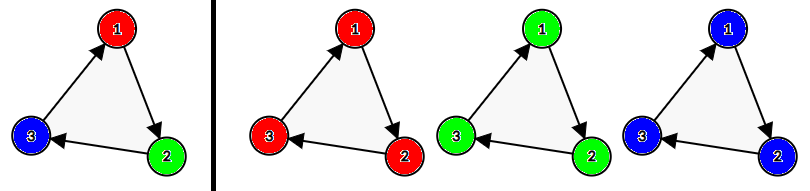
小 $\alpha$ 希望他喜欢的边与红色的点在模 $3$ 后数量一致,小 $\beta$ 给定了 $q$ 个点集,希望对于每个点集,在两个顶点均在点集中的边中,小 $\alpha$ 喜欢的边数与小 $\beta$ 喜欢的边数在模 $3$ 后一致。
小 $\alpha$ 与小 $\beta$ 已经告诉了小 $\gamma$ 满足他们条件的染色方案数 $s$,小 $\gamma$ 希望你能告诉他 $s \bmod 1000000007$ 的结果进行验证。我们称两个染色方案是不同的,当且仅当存在一个结点在两种染色方案中颜色不同。
实现细节
本题暂仅支持 C++。
由于输入量较大,为减少输入所需时间并减轻评测机压力,我们使用交互的形式进行输入输出,你无需关注交互库细节,评测用交互库运行所需时间空间预计与下发的样例交互库相近。
你需要包含头文件 color.h。
你可以调用下述函数:
int get_n();
int get_m();
int get_q();
int get_edge_num(const int u,const int v);
bool get_constraint(const int id,const int u);依次会返回 $n$,$m$,$q$,$u$ 至 $v$ 的有向边边数,小 $\beta$ 的第 $\mathrm{id}$ 个给出的点集中是否包含结点 $u$。你需要保证变量 $\mathtt{u}, \mathtt{v}$ 传入的参数在 $[1, n] \cap \mathbb N$ 中,变量 $\mathtt{id}$ 传入的参数在 $[1, q] \cap \mathbb N$ 中。交互库保证不会在函数调用过程中修改任何你定义的对象。
可以注意到你可以多次以相同的参数调用上述函数。
你需要实现下述函数解决题目描述中提到的问题:
int solve();你可以在 solve 函数中调用上面提到的函数以获取给定的数据,需要将答案即 $s \bmod \left(10^9 + 7\right)$ 作为返回值返回。
此外,你无需也不能实现主函数,不能定义以 grader 开头的命名空间。
转换器输入格式
由于样例交互库的输入格式不方便人工输入,下发了一个输入格式转换器,你可以以下述格式作为转换器的输入,转换器会将样例交互库的输入输出至 color.in。
题面中显示的输入数据均为转换前的输入格式,下发文件为样例交互库的输入格式。
第 $1$ 行 $2$ 个整数 $\mathtt{n\ m}$。
第 $2$ 行至第 $m + 1$ 行,第 $i + 1$ 行 $2$ 个整数 $\mathtt{u_i\ v_i}$,表示图的边集 $E$ 为所有 $i \in [1, m] \cap \mathbb N$,从 $u_i$ 到 $v_i$ 的有向边构成的可重集。
第 $m + 2$ 行 $1$ 个整数 $\mathtt{q}$。
第 $m + 3$ 行至第 $m + q + 2$ 行,第 $i + m + 2$ 行 $k_i + 1$ 个整数 $\mathtt{k_i\ p_{i, 1}\ \dots\ p_{i,k_i}}$,表示小 $\beta$ 给定的第 $i$ 个集合为 $\{p_{i, j} \mid j \in [1, k_i] \cap \mathbb N\}$。
样例交互库输出格式
$1$ 行 $1$ 个整数 $\mathtt{x}$,其中 $x = s \bmod 1000000007$。
样例一
input
5 5 1 2 1 3 4 2 3 5 1 3 0
output
90
样例二
input
9 14 1 3 2 4 5 1 2 3 3 4 3 4 4 2 6 5 2 4 2 4 3 5 7 8 8 6 6 9 3 5 1 2 3 4 8 4 1 5 6 3 2 1 8
output
702
explanation
题面中的样例均为原本的输入格式,转换后的样例见下发文件。
样例三
见下发文件,满足 $\textrm{subtask }2$ 的限制。
样例四
见下发文件,满足 $\textrm{subtask }4$ 的限制。
样例五
见下发文件,满足 $\textrm{subtask }7$ 的限制。
样例六
见下发文件,满足 $\textrm{subtask }11$ 的限制。
样例七
见下发文件,满足 $\textrm{subtask }12$ 的限制。
限制与约定
对于所有数据,保证 $1 \leqslant n \leqslant 4000, 0 \leqslant q \leq 2000$,相同的边不会出现超过 $2$ 次。
本题有十三个子任务。只有该任务下测试点全部通过才能得到该子任务的分数。
| 子任务编号 | 子任务分数 | 特殊限制 |
|---|---|---|
| $1$ | $5$ | $n \leqslant 10, m \leqslant 200, q = 0$ |
| $2$ | $15$ | 图在无向化后为一棵树,$n \leqslant 2000, m = n - 1, q = 0$ |
| $3$ | $5$ | $n, m \leqslant 50, q = 0$ |
| $4$ | $10$ | $n, m \leqslant 500, q = 0$ |
| $5$ | $10$ | $n \leqslant 2000, q = 0$ |
| $6$ | $5$ | $n, m \leqslant 50, q \leqslant 5$ |
| $7$ | $10$ | $n, m \leqslant 500, q \leqslant 5$ |
| $8$ | $5$ | $n \leqslant 2000, q \leqslant 5$ |
| $9$ | $5$ | $n \leqslant 2000, m = 0$ |
| $10$ | $10$ | $n, m, q \leqslant 50$ |
| $11$ | $10$ | $n, m, q \leqslant 500$ |
| $12$ | $5$ | $n \leqslant 2000$ |
| $13$ | $5$ | 无特殊限制 |
时间限制: $1.5\texttt{s}$(可以根据评测机速度修改)
空间限制: $1024\texttt{MiB}$
