题目背景
Soulist 发明了一种特别的“量子”数据结构,叫做 osu!list,现在他急需你来验证一下他的实现对不对。
题目描述
osu!list 可以维护一个 $1$ 到 n 的排列 $a$,同时支持以下四种操作:
给定下标 $i$,将所有满足 $a_j < a_i$ 的 $a_j$ 执行赋值操作 $a_j \leftarrow a_j + 1$,最后执行赋值 操作 $a_i \leftarrow 1$。
给定下标 $i$,将所有满足 $a_j > a_i$ 的 $a_j$ 执行赋值操作 $a_j \leftarrow a_j − 1$,最后执行赋值 操作 $a_i \leftarrow n$。
给定下标 $i,j(i \neq j)$,交换 $a_i$ 与 $a_j$ 的值。
给定下标 $l,r(1 \leq l \leq r \leq n)$,询问 $\sum_{i=l}^{r} a_i$ 的值。
为什么说这是一个“量子”数据结构呢?它的特点就是修改操作会产生多个状态, 具体而言每次修改操作都会给出一定额外的参数 $p$,该数据结构会将所有的当前状态都 复制 $M + 1$ 份($M = 998,244,353$), 而其中的 $p$ 份会执行该修改操作,而 $M + 1 − p$ 份会忽略这次操作,也即对 $a$ 没有任何影响。这样一来如果该次修改操作发生之前有 $t$ 个状态,那么该次修改操作发生之后就会有 $(M + 1)t$ 个状态。
如此一来询问显然不能给出所有状态的答案,所以这个数据结构会给出对于所有状态执行该次询问的答案之和对 $M$ 取模后的结果。
虽然你唯一接触到量子计算就是上次 NOI 冬令营听的量子计算讲座,而且你当时直接翘掉了该活动, 但是迫于 Soulist 的压力,你还是不得不写一个程序来实现 osu!list 的功能。
输入格式
输入第一行两个正整数 $n,m$ 分别表示排列的长度与操作次数。
接下来输入一行 $n$ 个正整数 $a_1 , a_2 , ... , a_n$,表示排列的初始情况, 保证输入是一个 $1$ 到 $n$ 的排列。
接下来 $m$ 行,每行若干个整数描述一次操作,具体而言有下面几种情况:
1 i p表示以 $p$ 的额外参数对 $i$ 执行操作 $1$(见问题描述),保证 $1 \leq i \leq n, 0 \leq p < M$。2 i p表示以 $p$ 的额外参数对 $i$ 执行操作 $2$(见问题描述),保证 $1 \leq i \leq n, 0 \leq p < M$。3 i j p表示以 $p$ 的额外参数对 $i,j$ 执行操作 $3$(见问题描述),保证 $1 \leq i, j \leq n, i \neq j, 0 \leq p < M$。4 l r表示对 $l,r$ 执行操作 $4$(见问题描述),保证 $1 \leq l \leq r \leq n$。
输出格式
对于每次询问操作,你需要输出一行表示该次询问的答案(对 $M$ 取模)。
样例
【样例输入 1】
4 3
3 4 1 2
3 2 4 1
1 1 499122177
4 2 4【样例输出 1】
8【样例 1 解释】
一开始数组为 $3,4,1,2$:
第一次操作以参数 $1$ 交换 $a_2,a_4$,得到 $1$ 个状态为数组 $3,2,1,4$,$M$ 个状态为数组 $3,4,1,2$。
第二次操作以参数 $499,122,177 = \frac{M +1}{2} 对位置 $1$ 执行操作 $1$,得到 $\frac{M +1}{2}$ 个状态为数组 $3, 2, 1, 4$,$\frac{M + 1}{2} 个状态为 $1, 3, 2, 4$,$\frac{M(M + 1)}{2}$ 个状态为 $1, 3, 2, 4$,$\frac{M(M + 1)}{2}$ 个状态为 $3, 2, 1, 4$。
第三次操作询问所有状态 $a_2 + a_3 + a_4$ 的和对 $M$ 取模,为 $\frac{M+1}{2}(2+1+4)+\frac{M+1}{2}(3+2+4)+\frac{M(M+1)}{2}(3+2+4)+\frac{M(M+1)}{2}(2+1+4) \mod M =8$
【样例 2~7】
见下发文件,其中:
样例 3 满足特殊性质 A 和 B。
样例 4 满足特殊性质 A。
样例 5 满足特殊性质 B。
样例 6 满足特殊性质 C。
子任务
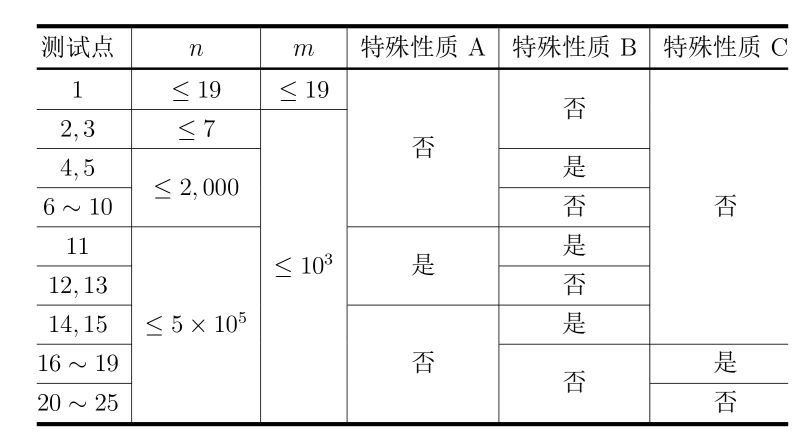
提示
现在还有人认识 Soulist 吗,我的锁老师不会过气了吧(流泪)。
