【题目背景】
要想见证尘封的秘密,就要承受最严厉的惩罚。
【题目描述】
给定正整数 $n$ 和质数 $p$。对于 $\{1, 2,\dots, n\}$ 的一个非空子集 $S$,称 $S$ 是好的, 当 且仅当 $S$ 中元素的最大公约数为 $1$ ,且最小公倍数为 $n$。
求好的集合的个数,答案对 $p$ 取模。
【输入格式】
本题的一个测试点中包含多组测试数据,它们的 $p$ 相同。
第一行两个正整数 $T, p$,表示测试数据组数和模数。
接下来 $T$ 行,每行一个正整数 $n$,表示一组测试数据。
【输出格式】
输出 $T$ 行,每行一个正整数,表示该组测试数据的答案。
【样例 1 输入】
4 998244353
6
60
25200
698377680【样例 1 输出】
7
3464
343008195
181431013【样例 1 解释】
对于第一组数据, 好的集合为 $\{1, 2, 3, 6\}, \{2, 3, 6\}, \{2, 3\}, \{1, 3, 6\}, \{1, 6\}, \{1, 2, 6\}$ 和 $\{1, 2, 3\}$,共 7 个。
【样例 2 输入】
20 998244353
18
66
200
30030
355630
795240
3703590
3873270
23423400
39859397
54146162
280619892
918430227
23027612400
55359422200
170576560440
430722790638
484161811172
487231668000
757598055555【样例 2 输出】
32
193
2852
306800760
301343741
433428976
594912666
306800760
958096256
16625216
306800760
492717383
267114429
173804191
826198479
281595478
492717383
753502088
7467789
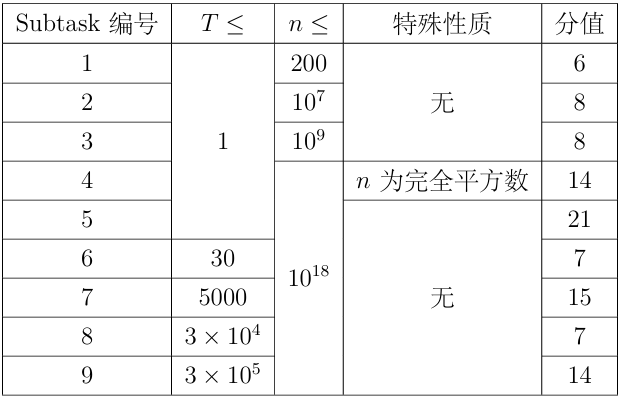
249502816【数据范围】
对于所有测试点: $1 \leq T \leq 3 \times 10^5 , n\leq 10^{18} , p \in [10^8 , 10^9 + 7]$,保证 $n$ 的最大质因 子不超过 $100$。
【提示】
你可以使用 barrett 取模优化加速取模运算,下发文件中提供了一份示例代码。
