题目描述
给定一张 $n$ 个点、$m$ 条边的无向图。边 $e$ 的长度为二元组 $(c_e, t_e)$。
一条途径 $w$ 的长度 $(c_w, t_w) = (\sum_{e \in w} c_e, \sum_{e \in w} t_e)$。
一条途径 $w$ 比另一条途径 $w'$ 短,当且仅当二者长度不同且 $c_w \le c_{w'}, t_w \le t_{w'}$。
显然可能有两条途径无法比较长短,进而两点间可能出现多条长度不同的最短路径。
求 $s$ 至 $e$ 的最短路径的长度取值的种类数。
输入格式
第一行四个整数 $n, m, s, e$。
接下来 $m$ 行,每行四个整数 $p, r, c, t$,分别表示一条边的两个端点与长度。
输出格式
一行一个整数,你的答案。
样例 #1
样例输入 #1
4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4样例输出 #1
2提示
样例说明
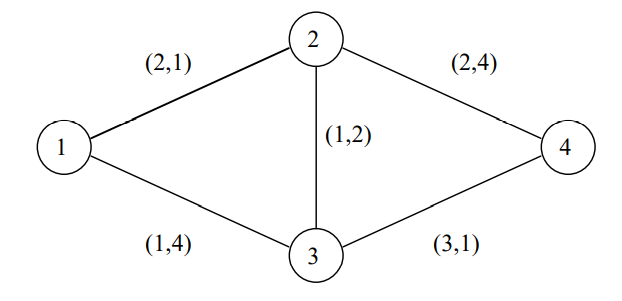
考虑其中四条途径:
- $1 \to 2 \to 4$(长度为 $(4, 5)$);
- $1 \to 3 \to 4$(长度为 $(4, 5)$);
- $1 \to 2 \to 3 \to 4$(长度为 $(6, 4)$);
- $1 \to 3 \to 2 \to 4$(长度为 $(4, 10)$)。
途径 0、途径 1 均短于途径 3。最短路长度共有两种:$(4, 5)$(途径 0、途径 1)、$(6, 4)$(途径 2)。
数据范围
$1 \le s, e, p, r \le n \le 100$,$0 \le m \le 300$,$s \ne e$,$0 \le c, t \le 100$。
