【题目描述】
小 B 和小 L 坐在一棵树下。阳光被层层叠叠的树叶过滤,漏到他们身上变成了淡淡
的圆圆的轻轻摇曳的光晕。
小 B 突然笑道「我想到了一个很有趣的问题」
「是什么样的问题呢?」小 L 问道。
小 B 抬起头看向远方,轻轻说到「你想,假如平面上有 n 个点和 m 条无向边……」
「所以问题是什么呢?」小 L 打断他「我们直接跳过这些老生常谈的东西吧」
小 B 将目光投向小 L,「不要这么着急嘛。假如你要从某个点出发走出一条欧拉回
路,同时还要求转过的角度之和尽量小。那么怎么找出这个最小的角度呢?」
「转过的角度……这是什么意思」小 L 问道「你是说,相邻两条边的角度吗」
「不完全是」小 B 拿起一根树枝「你看,像这样……」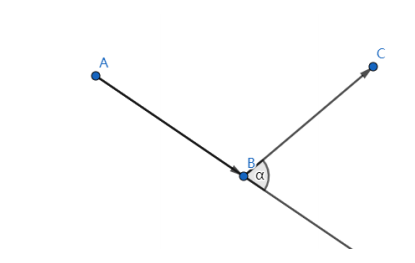
「假如要从 A 走到 B,再从 B 走到 C。那么你转过的角度就是 α,而转过的角度之
和就是所有这样的 α 之和」
小 L 托腮深思「听起来像是一个有趣的问题」
一阵风吹动两人的衣袖,树叶沙沙作响,光影在地上摔成斑驳的碎片。
良久之后小 L 说道「但是看起来这个问题可以从 3-SAT 规约过来的样子……我不是
很会做一般情况」
小 B 说道「先不管能否规约 3-SAT,这个问题在某些特殊性质下是非常好做的……
比如每个点的度数都不超过 4」 小 L 思考片刻「我理解你的意思了,那这个问题已经完全是一道 OI 题了!」
他们将这个问题给了你,请你解决这个问题。
【输入格式】
第一行两个正整数 n, m ,分别代表点数和边数。
接下来 n 行,其中第 i 行两个非负整数 xi
, yi,表示第 i 个点的坐标是 (xi
, yi)。
之后有 m 行,其中第 i 行两个正整数 ui
, vi,表示第 i 条无向边连接了第 ui 和第 vi
个点。
【输出格式】
输出到文件 noname.out 中。
一行一个小数,表示转过角度之和的最小值(弧度制)。你的答案与标准答案的绝对
或相对误差不能超过 $10^{−5}$。
【样例 1 输入】
4 4 0 0 1 0 1 1 0 1 1 2 2 3 3 4 4 1【样例 1 输出】
1 6.283185【样例 2 输入】
8 12 1 4 3 2 5 3 7 2 9 5 6 6 4 5 2 5 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 1 3 7 7 2 3 6 2 6【样例 2 输出】
1 16.635258【样例 2 解释】 下图为样例 2 所对应的图像:
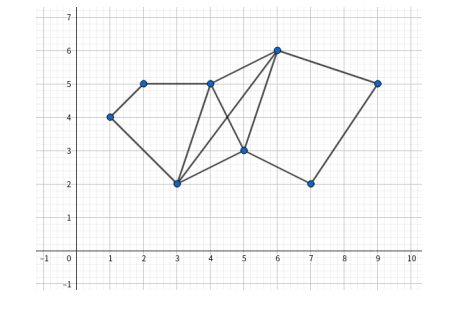
【样例 3】 见选手目录下的 noname/noname3.in 与 noname/noname3.ans。
【测试点约束】 对于所有测试数据:$1 ≤ n ≤ 10^5 , n − 1 ≤ m ≤ 2n, 0 ≤ xi , yi ≤ 10^9$。保证图连通且不 存在自环。保证存在欧拉回路。保证不存在某个点的度数大于 4。
本题评测开启捆绑测试。

