【题目描述】
Number 10 Downing Street 的建筑结构可以抽象地看成一张简单无向图,没有重边
自环。Humphrey Appleby 为了阻止 Jim Hacker,决定最大化他行走所需的时间。具体
地,他希望对每个点 i 给其邻接边安排一个顺序(一条无向边 (a, b) 既是 a 的邻接边,也
是 b 的邻接边),我们称其为边 (x, i) 关于 i 的编号,记为 rki(x)。
编号之后,Humphrey Appleby 希望这张图满足以下条件:
对于 .所 .有 .环 a1, a2, a3, · · · , am(存在边 (a1, a2),(a2, a3), · · · ,(am, a1),令 a0 = am, am+1 = a1),有 ∀i ∈ [1, m], rkai (ai−1) < rkai (ai+1) 或 ∀i ∈ [1, m], rkai (ai−1) > rkai (ai+1)。
你需要帮助 Humphrey Appleby 构造一个合法的编号方案。但是由于建筑结构复杂,
上过牛津的 Humphrey Appleby 也搞不清到底存不存在解,因此还需要你判断是否无解。
【输入格式】
从文件 granddesign.in 中读入数据。
第一行一个数 T。
接下来 T 组数据。
每组数据第一行一个数 n, m。分别表示简单无向图的点数和边数。
接下来 m 行每行两个数 x, y。表示一条无向边 (x, y)。
【输出格式】
输出到文件 granddesign.out 中。
第一行一个字符串 YES 或 NO 表示是否存在解。
如果存在解,第 i + 1 行输出 i 的度数个正整数,第 j 个表示 i 的编号为 j 的出边的
另一端 x。
如果存在多组解,输出将方案的每一行依次拼接后 .字 .典 .序 .最 .小的那个。
【样例 1 输入】
1 4 4 1 2 2 3 3 4 4 1【样例 1 输出】
YES 2 4 3 1 4 2 1 3【样例 2】
见选手目录下的 granddesign/granddesign2.in 与 granddesign/granddesign2.ans。
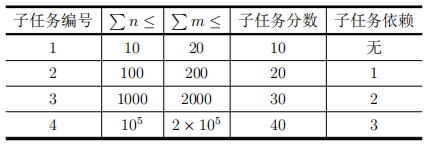
【测试点约束】
对于所有测试数据:$1 ≤ n ≤ 10^5 1 ≤ m ≤ 2 × 10^5,∑n ≤ 10^5,∑m ≤ 2 × 10^5。$
本题评测开启捆绑测试。