【题目描述】
贝拉准备开一家玩偶商店，她有 n 种玩偶，第 i 种玩偶的价值为 vi。她知道对于第 i 种玩偶而 言，嘉然有一个喜好参数 wi（特别的，i = 0 表示什么都不买），这个参数会在一个实数区间 [li , ri]$ 里 浮。
贝拉想选择一个非空玩偶集合 S 卖出，使得最坏情况下嘉然进店消费的期望最大。嘉然买第 i \in S 种玩偶的概率是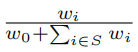，不买的概率是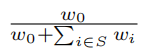。最坏情况指在 w 所有可能的取值中使得期 望最小的情况。
随着时间，会发生 m 次变化，贝拉的玩偶或者嘉然的喜好程度将会发生惊天变化：
1. 1 i L R 向晚带嘉然游山玩水，第 i 个玩偶的喜好区间变成 [L, R]。
2. 2 i V 乃琳加工了第 i 个玩偶，它的价值变为 V 。
变化会一直持续，你要回答初始以及每次变化后最坏情况下嘉然进店消费的最大期望，你需要以 最简分式（可以证明是一个有理数）的形式输出。
【输入格式】
从文件 doll.in 中读入数据。
第一行包括两个数 n, m。第二行 n 个数，第 i 个数表示 vi。第三行 n + 1 个数，第 i 个数表示 li−1。第四行 n + 1 个数，第 i 个数表示 ri−1。接下来 m 行表示操作，形式如 1 i L R 或者 2 i V。
【输出格式】
输出到文件 doll.out 中。
共 m + 1 行，每行输出一个 a/b ，按顺序表示初始以及每次修改后的最大期望，你需要以最简分 式（可以证明是一个有理数）的形式输出。
【样例输入】

2 5
4 2
4 3 2
4 3 2
2 1 2
1 1 2 3
1 0 0 0
1 1 0 0
1 2 0 0

16/9
10/9
1/1
2/1
2/1
0/1