1.1 问题描述
对于一个简单无向图 G = (V, E),定义它的一个点覆盖为一个点的子集 S ⊆ V ,并且对于每条
边 (u, v) ∈ E,满足 u ∈ S ∨ v ∈ S。图 G 的最小点覆盖为最小的 S 满足如上条件。
你需要统计有多少 n 个点的简单无向图的最小点覆盖大小恰好为 k。两个图 G1, G2 不同当且仅
当存在 (u, v) ∈ E1 但 (u, v) ̸∈ E2。
因为一些原因,本题有多组数据,并且你只需要输出答案模 2 的余数。
1.2 输入格式
第一行一个正整数 T(1 ≤ T ≤ 256),表示数据组数。
然后 T 行,每行一组数据,包含两个整数 n, k(1 ≤ n < 256, 0 ≤ k ≤ n),含义与题面相同。
1.3 输出格式
输出共 T 行,每行一个整数,第 i 行的数表示第 i 组数据的答案模 2 的余数。
1.4 样例 1 输入
20 3 1 5 4 5 3 5 2 97 0 97 1 97 2 242 0 242 1 242 2 17 3 18 15 14 7 13 5 12 4 252 29 227 79 241 152 191 177 196 1791.5 样例 1 输出
0 1 1 0 1 1 0 1 1 0 0 1 1 1 1 0 0 1 0 11.6 样例解释
样例解释:前两组数据的真实答案分别为 6 和 1。
大样例
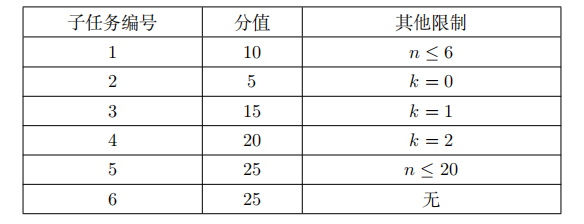
1.7 数据规模与约定