题目描述

一个 $10^6\times 10^6$ 的网格图上有 $n$ 头牛、$m$ 朵花、和 $p$ 个围栏。每个牛和花占据 $1\times 1$ 的格子，而每个围栏占据一个矩形。
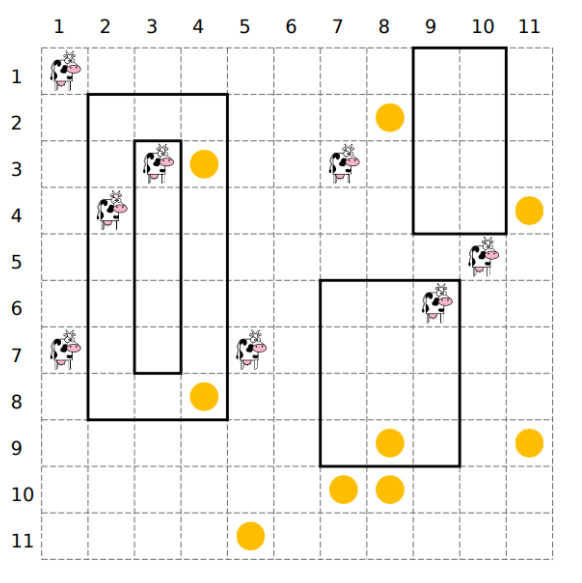
围栏所代表的矩形由 $(r1,c1,r2,c2)$ 给出，代表左上角为 $(r1,c1)$、右下角为 $(r2,c2)$，例如下图中的4个矩形为：$(2,2,8,4),(1,9,4,10),(6,7,9,9),(3,3,7,3)$
特别地，在本题中所有围栏矩形仅可能相离或者包含、而不会相交或接触。例如不会出现 $(1,1,2,2),(2,2,3,3)$， $(1,1,2,2),(3,3,4,4)$，$(1,1,3,3),(4,1,6,2)$ 等情况。

给定所有牛、花、围栏的位置，牛仅可以向右、向下走，牛可以跨越其他牛或者花的位置、但不能跨越 围栏。
请问对于每只牛，有多少朵花的位置是它可以走到的。

输入格式

第一行1个整数 $f$，代表围栏数量
接下来 $f$ 行，每行4个整数 $(r1,c1,r2,c2)$ 代表一个围栏
接下来1个整数 $m$，代表花的数量
接下来 $m$ 行，每行2个整数 $(r,c)$ 代表一朵花的位置，保证花的位置各不相同
接下来1个整数 $n$，代表牛的数量
接下来 $n$ 行，每行2个整数 $(r,c)$ 代表一头牛的位置，保证牛的位置各不相同、且牛和花不会处于同一位置

输出格式

输出 $n$ 行，第 $i$ 行的整数代表第 $i$ 头牛能走到的位置包含多少朵花。

样例

样例1输入

4
2 2 8 4
1 9 4 10
6 7 9 9
3 3 7 3
9
3 4
8 4
11 5
10 7
10 8
9 8
2 8
4 11
9 11
8
1 1
5 10
6 9
3 7
7 1
4 2
7 5
3 3

样例1输出

5
1
0
1
3
1
3
0

样例1解释

见题目描述中的图片。

样例2

见下发样例。

数据范围

对于 $100\%$ 的数据，满足 $1\leq f,m,n \leq 2\times 10^5$，$1\leq r1,c1,r2,c2,r,c \leq 10^6$ ，保证围栏不相交或 接触，保证牛和花的位置互不相同，保证一个位置上不会同时存在牛和花。 子任务1（15分）：$r1,c1,r2,c2,r,c \leq 1000$
子任务2（15分）：$f=0$
子任务3（15分）：$f,n,m \leq 1000$
子任务4（15分）：$n\leq 500$
子任务5（40分）：无特殊限制