题目描述
一个 n m的网格,c [ i ][j] 代表(i,j) 位置的颜色,初始所有c [ i ][j]=0 ,代表全部为白色。
若两个格子之间有公共边,则称它们【边相邻】,例如和 边相邻的格子最多有4个:
(i-1,j),(i,j-1).(i+1,j),(i,j+1)。
若两个格子之间没有公共边、但是有公共角,则称它们【角相邻】,例如和 (i,j)角相邻的格子最多有4
个:(i-1,j-1),(i-1,j+1).(i+1,j-1),(i+1,j+1) 。
有 k次刷墙操作,每次选择连续的若干整行、或者连续的若干整列,把它们刷成颜色 col[i](
$0\le col[i] \le k$,注意col[i]=0 代表白色)。
同传统的刷墙题一样,后刷的颜色会覆盖之前的颜色。
在完成全部刷墙操作之后,请你统计有多少对格子边相邻且颜色相同,有多少对格子角相邻且颜色相
同。
输入格式
第一行4个正整数n,m,k,tp ,代表网格大小、操作次数,以及询问类型(见输出格式)
接下来k 行,每行4个整数 op,l,r,col代表一次刷墙操作,若 op=0代表将第l~r 行全部刷成col
颜色,若op=1 代表将第l~r 列全部刷成 col颜色。
输出格式
输出1个整数代表答案。
若 tp=0,仅输出有多少对格子边相邻且颜色相同;
若 tp=1,输出有多少对格子边相邻且颜色相同、或者角相邻且颜色相同。一对格子只统计1次。
样例
*样例1输入
3 4 4 0 0 2 3 2 1 2 4 0 1 3 3 2 0 1 1 0样例1输出
9样例2输入
3 4 4 1 0 2 3 2 1 2 4 0 1 3 3 2 0 1 1 0样例2输出
12样例3~4
见下发样例。
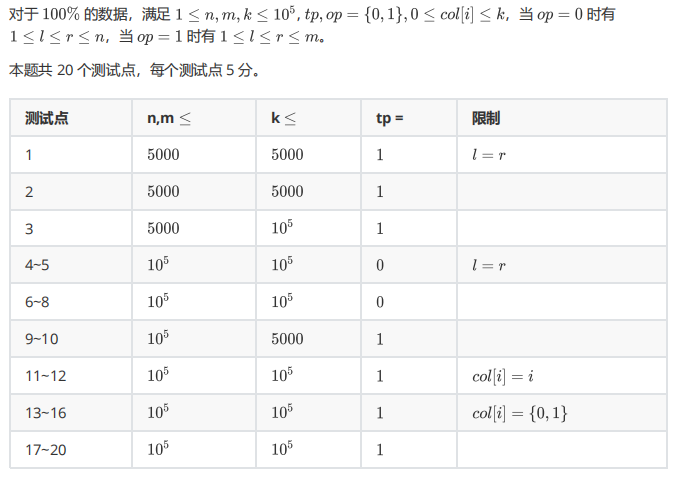
数据范围