【题目描述】
给定平面内的 n 个矩形,求满足 1 ≤ i < j < k ≤ n 且矩形 i, j, k 两两不交的三元
组 (i, j, k) 的数量。
【输入格式】
从文件 lycoris.in 中读入数据。
第 1 行包含 1 个正整数 n,表示矩形个数。
接下来 n 行,第 i 行包含 4 个整数 li
, ri
, di
, ui,表示第 i 个矩形的左边界、右边界、
下边界和上边界。
保证$ ∀i \ne j, li\ne lj
, ri\ne rj
, li\ne rj
, di\ne dj
, ui\ne uj
, di\ne uj。$
【输出格式】
输出到文件 lycoris.out 中。
输出 1 个非负整数,表示答案。
【样例 1 输入】
5 1 5 1 5 4 8 2 6 3 7 3 7 2 6 28 32 42 46 42 46【样例 1 输出】
3【样例 2 输入】
6 1 8 6 10 2 5 3 12 3 4 15 20 0 9 2 22 -5 22 -2 23 -7 11 -1 17【样例 2 输出】
0【样例 3 输入】
10 -114 -46 148 199 -27 187 -26 190 -64 -16 151 228 -162 -44 -107 -96 45 185 -197 -128 100 180 -23 222 -152 138 52 181 141 193 -109 87 -87 175 -35 123 -110 227 -73 -44【样例 3 输出】
41【样例 4】
见选手目录下的 lycoris/lycoris4.in 与 lycoris/lycoris4.ans。
【样例 5】
见选手目录下的 lycoris/lycoris5.in 与 lycoris/lycoris5.ans。
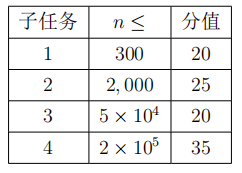
【子任务】
.本 .题 .开 .启 .捆 .绑 .测 .试。
对于所有数据,$1 ≤ n ≤ 2 × 10^5, −10^9 ≤ li < ri ≤ 10^9, −10^9 ≤ di < ui ≤ 10^9。 ∀i\ne j, li\ne lj , ri\ne rj , li\ne rj , di\ne dj , ui\ne uj , di\ne uj。$