[title]Description[/title]
　　经典的最小费用最大流问题是这样的。我们需要把一些石油从产油地s运往耗油地t，途中有若干根有向的管道，每根管道有一个容量上限cap，即最多有cap单位的油这根管道经过；每根管道还有一个费用cost，每单位油从这根管道经过需要花费cost的钱。你需要求出在输油量最大的前提下，最少花费多少钱。
　　现在我们的有向图如下图。

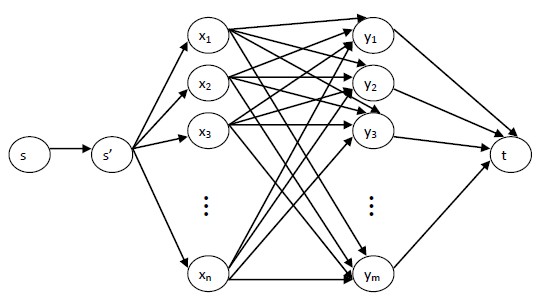
　　每个点没有容量限制，且石油经过点都不需要任何花费。
　　图中有4类边。第一类为s到s’的边，其流量为A，费用为0；第二类为s’到xi的边，其容量为Bi，费用为Ci；第三类为xi到yj的边，其容量为Di,j，费用为$E_{i,j}$；第四类为$y_j$到t的边，其容量为正无穷，费用为Fj。

[title]Input[/title]
　　输入第一行有3个正整数，n,m,A，分别表示图中x类点的个数、y类点的个数和题目叙述中的A。
　　第二行有2n个正整数，第2i-1个数和第2i个数(1≤i≤n)表示题目中的Bi和Ci。
　　第三行有m个正整数，第j个数(1≤j≤m)表示题目中的Fj。
　　接下来n行，每行2m个正整数。第i行(1≤i≤n)第2j-1个数和第2j个数(1≤j≤m)分别表示Di,j和Ei,j。

Output
　　一行两个整数，最大的流量和流量最大时最小的费用。
Sample Input
3 2 3
3 2 2 1 10 2
1 1
3 2 3 3
1 1 3 2
10 4 10 5

Sample Output
3 12

[title]Hint[/title]
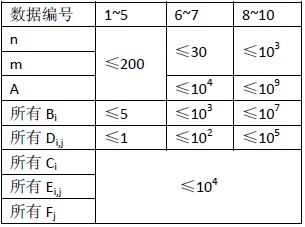
　　每个测试点的数据规模如下