【问题描述】
T 城是一个旅游城市,具有 n 个景点和 m 条道路,所有景点编号 1, 2, ..., n。每条道路连接这 n 个景区中的某两个景区,道路是单向通行的。每条道路都有一个长度。为了方便旅游,每个景点都有一个加油站。第 i 个景点的加油站的费用为 pi,加油量为 ci。若汽车在第 i 个景点加油,则需要花费 pi 元钱,之后车的油量将被加至被加至油量上限与 ci 中的较小值。不过如果加油前汽车油量已经不小于 ci,则不能在该景点加油。
小 C 准备来到 T 城旅游。他的汽车油量上限为 C。旅游开始时,汽车的油量为 0。在旅游过程中:
1、当汽车油量大于 0 时,汽车可以沿从当前景区出发的任意一条道路到达另一个景点(不能只走道路的一部分),汽车油量将减少 1; 2、当汽车在景点 i 且当前油量小于 ci 时,汽车可以在当前景点加油,加油需花费 pi元钱,这样汽车油量将变为 min{ci, C}。
一次旅游的总花费等于每次加油的花费之和,旅游的总路程等于每次经过道路的长度之和。注意多次在同一景点加油,费用也要计算多次,同样地,多次经过同一条道路,路程也要计算多次。
小 C 计划旅游 T 次,每次旅游前,小 C 都指定了该次旅游的起点和目标路程。由于行程不同,每次出发前带的钱也不同。为了省钱,小 C 需要在旅游前先规划好旅游路线(包括旅游的路径和加油的方案),使得从起点出发,按照该旅游路线旅游结束后总路程不小于目标路程,且剩下的钱尽可能多。请你规划最优旅游路线,计算这 T 次旅游每次结束后最多可以剩下多少钱。
【输入格式】
输入第一行包含四个正整数 n, m, C, T,每两个整数之间用一个空格隔开,分别表示景点数、道路数、汽车油量上限和旅行次数。
接下来 n 行,每行包含两个正整数 pi, ci,每两个整数之间用一个空格隔开,按编号顺序依次表示编号为 1, 2, ..., n 的景点的费用和油量。
接下来 m 行,每行包含三个正整数 ai, bi, li,每两个整数之间用一个空格隔开,表示一条从编号为 ai 的景点到编号为 bi 的景点的道路,道路的长度为 li。保证 ai ̸= bi ,但从一个景点到另一个景点可能有多条道路。
最后 T 行,每行包含三个正整数 si, qi, di 描述一次旅游计划,旅游的起点为编号为 si的景点,出发时带了 qi 元钱,目标路程为 di。
【输出格式】
输出 T 行,每行一个整数,第 i 行的整数表示第 i 次旅游结束后最多剩下多少元钱。
如果旅游无法完成,也就是说不存在从景点 si 出发用不超过 qi 元钱经过不小于 di 的路程的路线,则该行输出 −1。
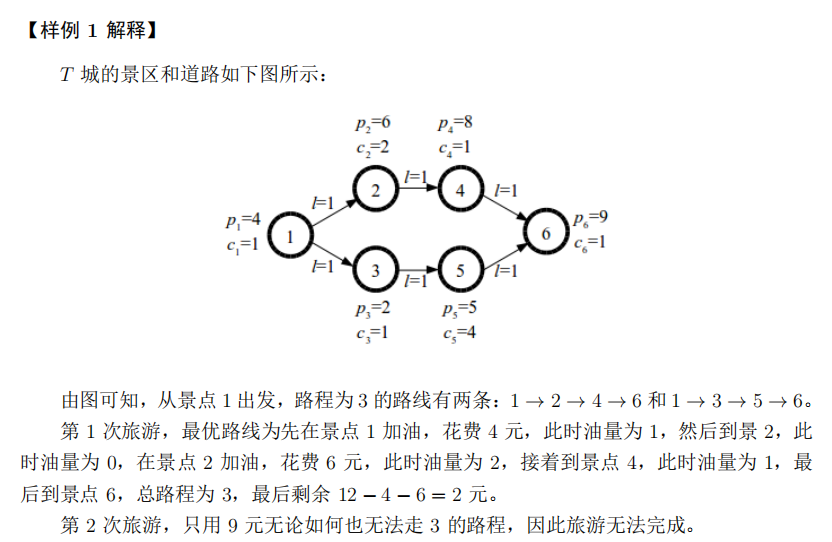
【样例 1 输入】 6 6 3 2 4 1 6 2 2 1 8 1 5 4 9 1 1 2 1 1 3 1 2 4 1 3 5 1 4 6 1 5 6 1 1 12 3 1 9 3 【样例 1 输出】 2 -1
大样例
【数据规模与约定】
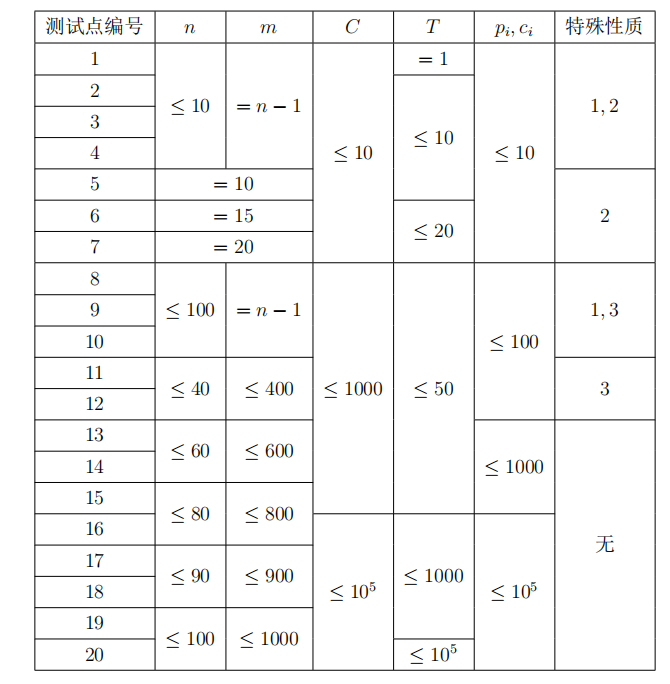
特殊性质 1:所有 ai = i, bi = i + 1, li = 1。
特殊性质 2:所有 di ≤$10^3$。
特殊性质 3:所有 qi ≤ 100。
对于所有数据,$2 ≤ n ≤ 100, 1 ≤ m ≤ 1000, 1 ≤ C, T ≤ 10^5, 1 ≤ ai, bi, li ≤ n 1 ≤ pi, ci ≤ 10^5, 1 ≤ si ≤ n, 1 ≤ qi ≤ n2, 1 ≤ di ≤ 10^9$。
