【题目描述】

你是一名优秀的星际指挥官。 某天，你开始检视星际地图，由于你数学很好，所以你定义了一张有许多性质的地图，编号为 $i$ 的星系会向编号为 $i$ 的真约数的星系连边。毫无悬念的，你发动了一场战争。你能够通过跃迁到达敌国任意一个地方。但跃迁引擎需要冷却，跃迁只能用一次。 你会直接占领跃迁到的星系，然后向外占领其他星系。一个星系 $u$ 能攻占星系 $v$ 当且仅当存在星系 $u$ 向星系 $v$ 的直接连边；你能占领星系 $v$ 当且仅当存在一个星系 $u$ 你已占领且星系 $u$ 能攻占星系 $v$ （跃迁到的星系除外）。当然，一个星系无法被重复占领，攻占它的星系是唯一的（跃迁到的星系被直接占领，而不被任何星系攻占）。 但由于你非常强，不满足于占领所有星系，所以给自己占领的星系加了些限制：由一个星系攻占的所有星系的编号要两两互质。 打完战争后，所有占领的星系间的单向边都被打通成双向边了。但由于你的兵力不足，不能将所有占领的星系都派军镇守。一个星系能派军镇守当且仅当它已占领。又为 了保证领土安全，你想到了一个绝佳的主意：派军镇守的星系间不能有直接连边。 派军镇守星系 $i$ 有收益 $a_i$ ，你想知道能获得的最大收益。

形式化地：给定 $n$ ，定义一个有向图 $G$ ，$G$ 中存在一条有向边 $(i, j)$ 当且仅当 $j|i$ 且 $i\ne j$ 。对于第 $i$ 个点，点权为 $a_i$ 。定义一颗外向树的权值为这颗外向树的点权最大独立集（外向树为空时权值为 0 ）。规定外向树 $T$ 是合法的当且仅当所有深度相同的节点的编号两两之间互质。求所有 $G$ 的联通子图的合法外向生成树 $T$ 的最大权值（子图可以为空集）。

外向树的定义是一棵有根树，满足所有边都是由父亲指向儿子的有向边。 独立集的定义是集合内每两个点之间都没有边，点权最大独立集是点权之和最大的 一个独立集。

【输入格式】

从文件 war.in 中读入数据。 第一行包含一个正整数 $n$。 第二行包含 $n$ 个整数 $a_{1...n}$。

【输出格式】

输出到文件 war.out 中。 输出包含一行一个整数，表示最大权值。

【测试点约束】

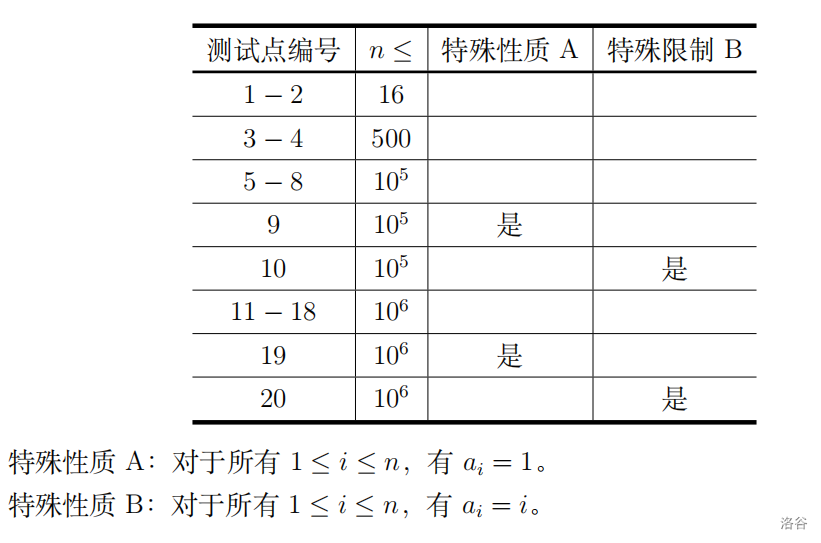
对于所有的数据，有 $1 ≤ n ≤ 10^6$，$|a_i| ≤ 10^9$。 每个测试点的具体限制见下表：