魔法少女（kisara） - Problem - Universal Online Judge

题目背景

多年之后，$\stackrel{\mathrm{Ogata~Sh\bar{u}}}{绪方修}$先生 (男主) 终于找到了他的妹妹$\stackrel{\mathrm{Ogata Kanna}}{绪方环奈}$。不幸的是，环奈早已被恶魔附身，且被评定为 $\text{S}$ 级的恶魔附身者，一场大战即将展开。

[ 因为 $\text{Sponsor}$ 的原因省略了本应该出现在这里的 $\text{anime picture}$ ]

题目描述

请注意此题目描述中所有使用的量词，否则很有可能导致题目理解错误！

在贝隆市，每位恶魔附身者都有 $n$ 个战力评级，分别为 $a_1, a_2, ..., a_n$。$\stackrel{\mathrm{Kisara}}{木更}$小姐(下称梗小姐)也是如此。除此之外，由于梗小姐被评定为 $\text{A}$ 级的恶魔附身者，因此她有能力通过和绪方修先生接吻来将自己 $l$ 到 $r$ 之间的战力评级提升 $x$。

每轮梗小姐对环奈发起攻击时，她会根据 $l$ 到 $r$ 的战力评级来进行攻击。设 $l$ 到 $r$ 之间共有 $m$ 个数，则这轮攻击会持续 $\frac{m(m+1)}{2}$ 次。每一次梗小姐会选择一个本轮攻击还未选择过的子区间，即 $\sum_{l'=l}^r\sum_{r'=l'}^r$，并对环奈造成该子区间战力评级之和的平方,即 $(\sum_{i=l'}^{r'}a_i)^2$。由于梗小姐收到了魔法少女的庇护，每次攻击时会额外对环奈造成 $k\times (r'-l')\times a_{l'}a_{r'}$ 的伤害，其中 $k$ 为常数。在这里，我们定义 $k=r-l+2$（注意不是 $l'$ 和 $r'$）。

梗小姐将会告诉你接下来将会发生的 $q$ 次事件，她想知道，每一轮她对环奈发动攻击时，会对环奈造成多少的伤害，答案对 $998244353$ 取模。

我不知道会有人为了节约时间想看这么长的题目描述，所以在此提供本题的简要题意，希望能够帮助选手更好地理解本题:

有一个长度为 $n$ 的序列，你需要执行以下两种操作 $q$ 次:

操作 $1$: 给出 $l,r,x$，你需要将 $a_l,a_{l+1}, ..., a_r$ 的值加上 $x$。
操作 $2$: 给出 $l, r$，求 $$ \sum_{l'=l}^r\sum_{r'=l'}^r((\sum_{i=l'}^{r'}a_i)^2+k\times (r'-l')\times a_{l'}a_{r'}) $$

其中 $k=r-l+2$。

输入格式

第一行输入一个整数 $\text{type}$。

第二行输入两个整数 $n,q$，表示战力评级个数以及事件个数。

接下来一行，输入 $n$ 个整数 $a_1, a_2, ...a_n$，表示初始战力评级值。

接下来 $q$ 行，先输入一个整数 $\text{op}$，若为 $1$，再输入三个整数 $l, r, x$，表示梗小姐将自己 $l$ 到 $r$ 的战力评级提升 $x$；

若为 $2$，再输入两个整数 $l,r$，表示梗小姐会根据 $l$ 到 $r$ 的战力评级来对环奈进行一轮攻击，你需要回答这轮梗小姐会对环奈造成了多少的伤害，答案对 $998244353$ 取模。

由于本题需要支持强制在线，所以每次处理事件时，设上次询问的答案为 $\text{lstans}$，则对于第 $1$ 类事件，$l, r, x$ 均需要异或上 $(\text{lstans}\times\text{type})$ 才能得到真实的 $l, r, x$，对于第 $2$ 类事件，$l, r$ 均需要异或上 $(\text{lstans}\times\text{type})$ 才能得到真实的 $l, r$。

输出格式

对每一个第 $2$ 类事件，输出一行表示本次询问的答案。

样例输入 $1$

样例输出 $1$

样例 $1$ 解释

对于 $[1, 4]$ 之间的询问，它的子区间及计算的答案有:

[1, 1] => 1 * 1 + 5 * 0 * 1 = 1
[1, 2] => 3 * 3 + 5 * 1 * 2 = 19
[1, 3] => 6 * 6 + 5 * 2 * 3 = 66
[1, 4] => 10 * 10 + 5 * 3 * 4 = 160
[2, 2] => 2 * 2 + 5 * 0 * 4 = 4
[2, 3] => 5 * 5 + 5 * 1 * 6 = 55
[2, 4] => 9 * 9 + 5 * 2 * 8 = 161
[3, 3] => 3 * 3 + 5 * 0 * 9 = 9
[3, 4] => 7 * 7 + 5 * 1 * 12 = 109
[4, 4] => 4 * 4 + 5 * 0 * 16 = 16

最终答案为 $1 + 19 + 66 + 160 + 4 + 55 + 161 + 9 + 109 + 16 = 600$。

样例输入 $2$

0
10 8
7 4 1 8 6 4 7 9 4 5
2 1 5
1 6 9 4
2 4 6
2 1 10
1 1 10 5
2 3 3
2 9 10
2 1 10

样例输出 $2$

测试点约束

对于所有测试点：$\text{type} \in [0,1],1 \le n \le 528221,1 \le q \le 528221,1 \le l \le r \le n, 0 \le a_i,x < 998244353$。

每个测试点的具体限制见下表：

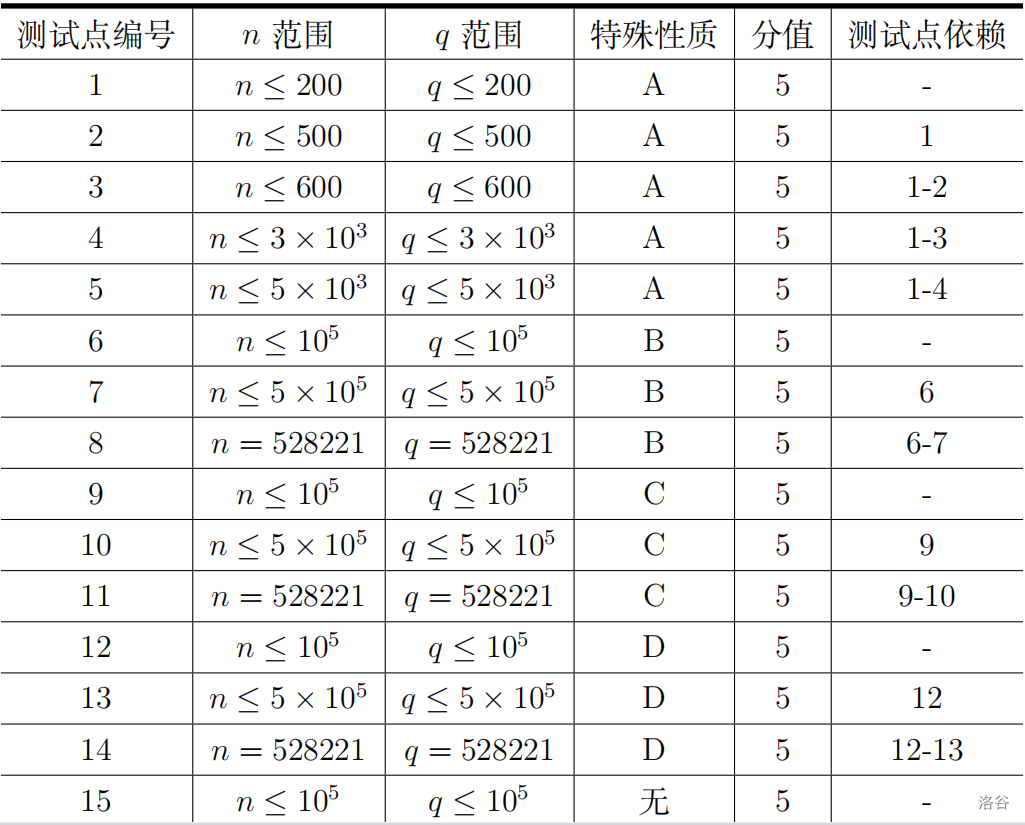
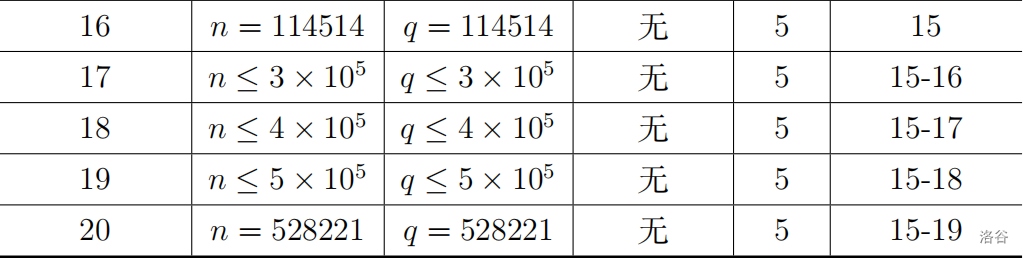
特殊性质 $A$: 对于所有的 $1 \le i \le q$，有 $\text{80%}$ 的概率 $op=2$，有 $\text{20%}$ 的概率 $op=1$

特殊性质 $B$: $\text{type} = 0$ 且对于所有的 $1 \le i \le q$，都有 $op=2$

特殊性质 $C$: 仅存在 $1$ 个 $1 \le i \le q$，使得 $op=2$

特殊性质 $D$: 对于所有的 $1 \le i \le q$，都有 $op=2$

Universal Online Judge

UOJ

新试题改错

M. 魔法少女（kisara）