题目描述

一场省选比赛拥有 $n$ 道题，对于选手小 M 来说，每道题目的他会以一定的概率 $p_i$ 通过。这样他的成绩可以用一个长度为 $n$ 的 01串来表示。$S_i=1$ 表示通过，反之表示不通过。一位选手在这种比赛中的总分为基本分与毗连分之和。 基本分的计算公式为（ $A$ 是给定的常数）： $ A\times \sum^n_{i=1} S_i$

而通过每道题的获得的毗连分则需要一个函数来计算（ $t$ 是给定的常数）： $$ f_i= \left\{ \begin{eqnarray} && S_i &&& i=1\\ && f(i-1)+1 ~~~ &&& i\not=1\wedge S_i=1\\ && f(i-1)\times t &&& \texttt{otherwise} \end{eqnarray} \right. $$

总毗连分的计算公式为 （ $B$ 是给定的常数）：$B\times (\sum^n_{i=1} S_if_i)$

为了让比赛更具有挑战性，出题人还会进行 $q$ 次操作。每次操作要么修改其中的一道题的通过概率 ，要么把一个区间的题目按照原来的顺序单独提出来作为一场比赛。出题人会告诉你每次修改的位置，以及修改后通过本题新的概率，你需要计算这位选手总分的期望，对 $998244353$ 取模。具体地，操作会具有以下两种格式：

• $0,x,wa,wb$ 表示将原来的 $p_x$ 修改为 $\frac{wa}{wb}$

• $1,l,r$ 表示询问对于从 $l$ 到 $r$ 的题目组成的比赛，小 M 的期望总分。

输入格式

第一行一个整数表示子任务编号。

第二行六个整数 $n,q,ta,tb,A,B$, 你需要计算得到 $t=\frac{ta}{tb}$，其余信息与题目描述中一致。

接下来 $n$ 行，每行两个整数 $pa_i,pb_i$， 你需要计算得到 $p_i=\frac{pa_i}{pb_i}$。

接下来 $q$ 行，每行一个操作，格式见问题描述。

输出格式

对于每个询问，输出一个整数表示期望得分。

样例

3
3 5 1 2 2 3
1 2
0 2
2 2
1 1 2
1 1 3
0 2 3 7
0 3 2 9
1 1 3

499122179
748683273
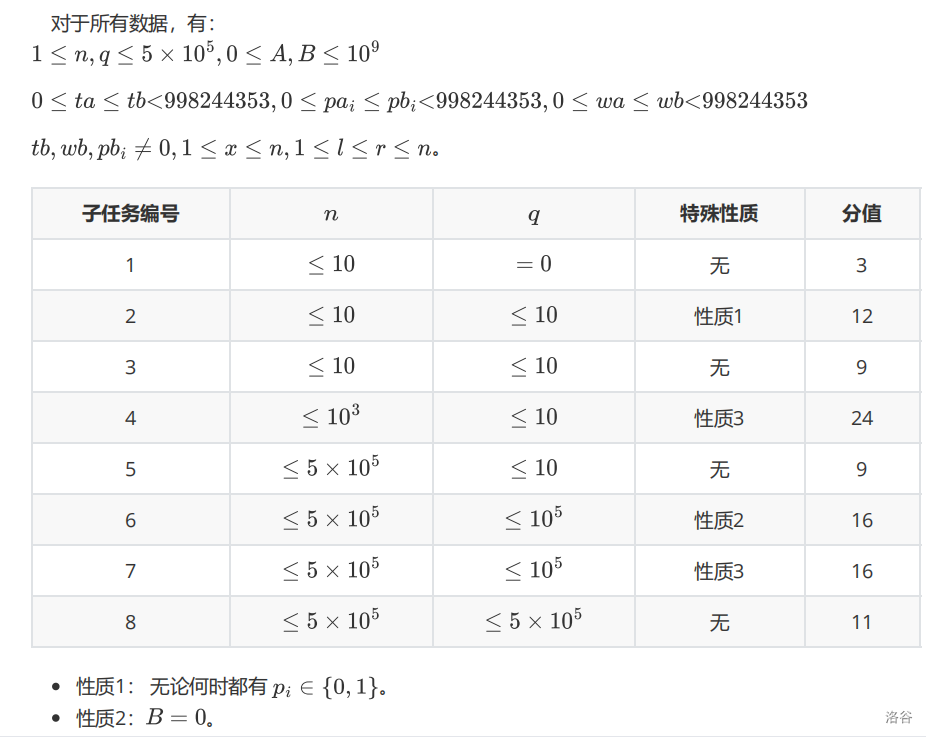
966554063

数据范围