在OI的上古时代,流传着这样一个故事:
有一天,小W到森林里游玩,回来之后跟小V说,我发现好多棵会动的树耶!小V说,这有什么好稀奇的,我用手指头就能维护每棵树的形态。
于是又过了几天小W到沙漠里游玩,回来之后跟小V说,我发现好多棵会动的仙人掌耶!小V说,这有什么好稀奇的,我用脚丫子就能维护每棵仙人掌的形态。
小S看到了这段故事,深受感动。他决定一步步做起,从仙人掌做起,从不会动的仙人掌做起。
本题中,我们定义:
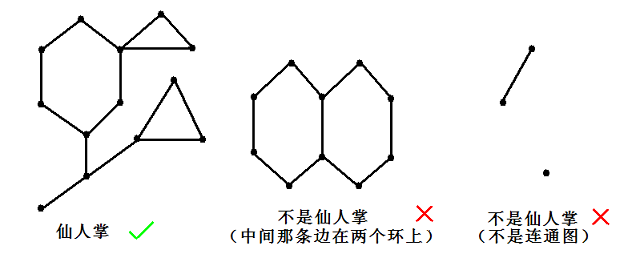
如果一个无向连通图的任意一条边最多属于一个简单环,且不存在自环,我们就称之为仙人掌。
仙人掌上的两点间最短路径(一定是简单路径)与最长简单路径的定义与一般无向图的定义相同。
本题中,我们还保证任何一个简单环的长度均为奇数。这意味着不存在重边,并且任意两点间的最短路径与最长简单路径一定是唯一的。
为了证明你确实能够维护仙人掌,我们给你 n 个结点,从 1 到 n 标号,其中 1 号点是仙人掌的根。它有 m 条边,第 i 条边连接了结点 ui 与 vi。
每个结点有一个颜色(黑或白),初始时均为黑色。现在有 q 次操作,每次操作格式为 op x(1≤op≤3,1≤x≤n):
若op=1,表示将点x到根的最短路径上的所有点的状态取反(黑变白,白变黑);
若op=2,表示将点x到根的最长简单路径上的所有点的状态取反;
若op=3,表示询问点x的子仙人掌中的黑点数目。点 x 的子仙人掌定义为:删除从根到点 x 的所有简单路径上的所有边后,点 x 所在的连通块。
输入格式
第一行三个用空格隔开的正整数 n,m,q 表示一共有 n 个结点,m 条边,q 个操作。
接下来 m 行,每行两个空格隔开的正整数 ui,vi,表示一条边。
接下来 q 行,每行表示一个操作,格式如上述。
输出格式 对于每个 op=3 的操作,输出一行相应的结果。
样例一 input
7 9 11
1 2
1 3
2 3
3 4
3 5
4 5
5 6
5 7
6 7
3 1
3 2
3 3
1 7
3 1
3 2
3 3
2 7
3 1
3 2
3 3output
7
1
5
3
1
2
4
0
3样例二
见样例数据下载。这组数据符合子任务4的限制与约定。
样例三
见样例数据下载。这组数据符合子任务5的限制与约定。
样例四
见样例数据下载。这组数据符合子任务6的限制与约定。
时间限制:1s。
空间限制:128MB。
n,q≤50000。
