题目描述
Mirko 在阁楼上发现了一块木板和 $n$ 个钉子。 Mirko 尽快将钉子钉在板上。 通过坐标平面对板进行建模,钉子作为其中的点。 没有两个钉子具有相同的 $x$ 或 $y$ 坐标。 为了继续玩乐,Mirko 偷走了姐姐的松紧发带,将其散布在所有的钉子上,然后放开。 松紧带自然在钉子周围收紧。
然后,Mirko 重复这些步骤,保证在板上至少留下三个钉子:
记录下由发圈围成的图形面积;
在板上选择最左边,最右边,最上面或最下面的钉子。
从板上卸下选择的钉子; 松紧带再次把仍留在板上的最靠外钉子绑起来。 现在我们知道 Mirko 在每次执行步骤 $2$ 时选择的钉子,编写一个程序来计算在每次执行步骤 $1$ 时计算出的图形面积的大小。
输入格式
第一行一个整数 $n$,表示钉子的个数。
接下来 $n$ 行,每行两个整数 $x_i$ 和 $y_i$,用空格隔开,表示第 $i$ 个钉子的坐标。
下面一行一个字符串,由 $n-2$ 个字符组成,这些字符可能为 L,R,U,D,分别表示 Mirko 选择拔掉的钉子。这四个字符的含义如下:
L表示拔掉最左边的钉子(横坐标最小的钉子);R表示拔掉最右边的钉子(横坐标最大的钉子);U表示拔掉最上方的钉子(纵坐标最大的钉子);D表示拔掉最下方的钉子(纵坐标最小的钉子)。
输出格式
共 $n-2$ 行,每行一个浮点数,表示每一次执行步骤 $1$ 时计算出的图形面积的大小,保留一位小数。
样例 #1
样例输入 #1
5
1 4
2 2
4 1
3 5
5 3
LUR样例输出 #1
9.0
6.5
2.5样例 #2
样例输入 #2
8
1 6
2 4
3 1
4 2
5 7
6 5
7 9
8 3
URDLUU样例输出 #2
34.0
24.0
16.5
14.0
9.5
5.0提示
样例 #2 解释:
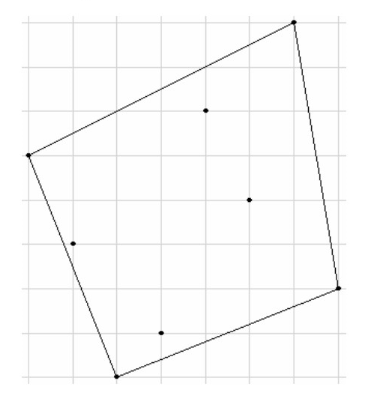
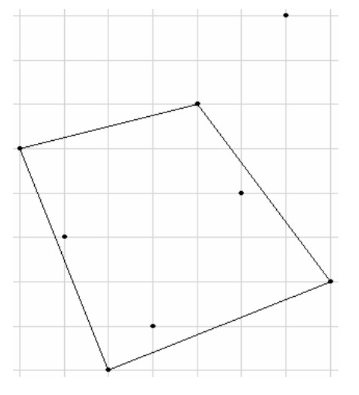
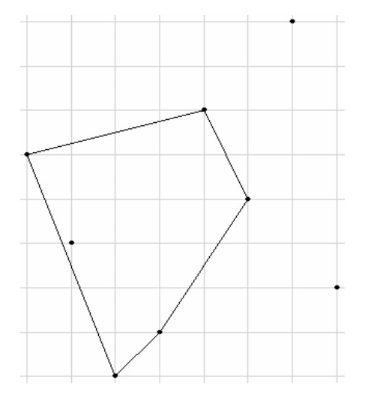
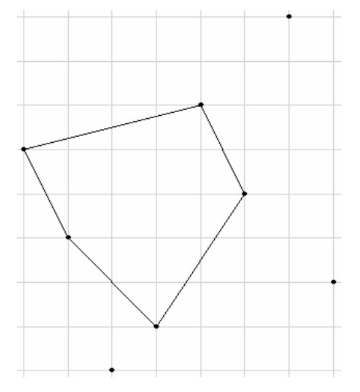
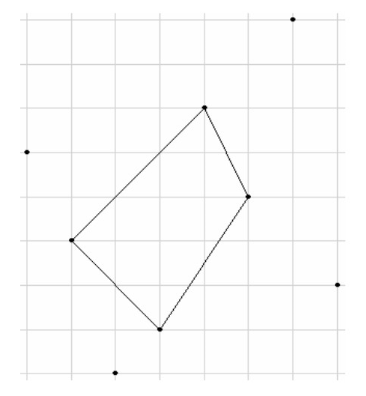
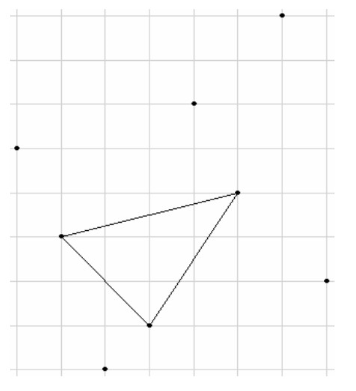
以上是对于样例 #2 的输入数据,程序应该按顺序模拟的六个步骤。
数据规模与约定
- 对于 $50\%$ 的数据,保证 $3 \leq n \leq 1000$。
- 对于 $100\%$ 的数据,保证 $3 \leq n \leq 3 \times 10^5$。
