组合数学自学资料
一.基本原理
1.加法原理:
做一件事有n类办法,则完成这件事的方法数等于各类方法数相加。
2.乘法原理:
做一件事分n步完成,则完成这件事的方法数等于各步方法数相乘。
注:做一件事时,元素或位置允许重复使用,求方法数时常用基本原理求解。
二.排列
排列:
从n个不同元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,所有排列的个数记为 ${A_n^m}$
三.组合
组合:
从n个不同元素中任取m(m≤n)个元素并组成一组,叫做从n 个不同的m 元素中任取 m 个元素的组合数,记作 ${C_n^m}$ 。
数学公式太多,不打了,学习资料和习题答案统一放在后面的压缩包中,做完后面的习题然后将答案用提交。分数为你正确答案个数/标准答案个数乘以100
题目:
填空题
1.电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种不同的播放方式(结果用数值表示).
2.6人排成一行,甲不排在最左端,乙不排在最右端,共有多少种排法? $\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $
3.有4个男生,3个女生,高矮互不相等,现将他们排成一行,要求从左到右,女生从矮到高排列,有多少种排法? $\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $
4.从4台甲型和5台乙型电视机中任取3台,其中至少要甲型和乙型电视机各一台,则不同的取法共有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种。
5.从5名男生和4名女生中选出4人去参加辩论比赛
(1)如果4人中男生和女生各选2人,有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $种选法;
(2)如果男生中的甲与女生中的乙必须在内,有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种选法;
(3)如果男生中的甲与女生中的乙至少要有1人在内,有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种选法;
(4)如果4人中必须既有男生又有女生,有 $\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种选法
(注意:每小问输出一行)
6.安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种.(用数字作答)
7.今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种不同的排法.(用数字作答)
8.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种(用数字作答).
9.要在如图所示的花圃中的5个区域中种入4种颜色不同的花,要求相邻区域不同色,有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种不同的种法(用数字作答).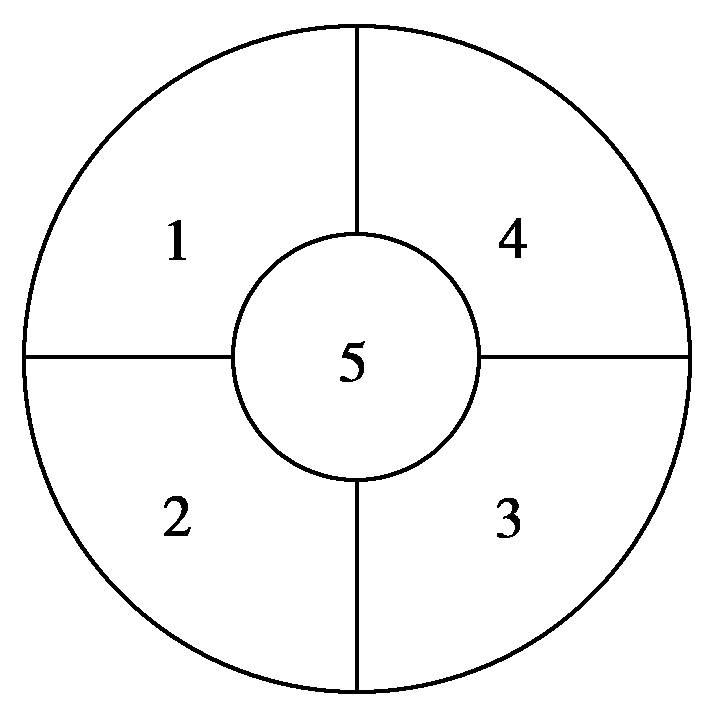
10.(天津卷(文))将3种作物种植在如图的5块试验田里,每块种植一种作物且相邻的试验田不能种植同一作物 ,不同的种植方法共$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $种(以数字作答)
| 1 | 2 | 3 | 4 | 5 |
|---|
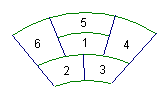
12.如图,用不同的5种颜色分别为ABCDE五部分着色,相邻部分不能用同一颜色,但同一种颜色可以反复使用也可以不用,则符合这种要求的不同着色种数.
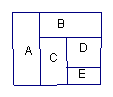
13.如图四个区域坐定4个单位的人,有四种不同颜色的服装,每个单位的观众必须穿同种颜色的服装,且相邻两区域的颜色不同,不相邻区域颜色相同,不相邻区域颜色相同与否不受限制,那么不同的着色方法是$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $ 种
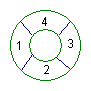
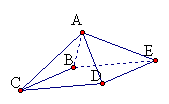
14.将一四棱锥(图6)的每个顶点染一种颜色,并使同一条棱的两端点异色,若只有五种颜色可供使用,则不同的染色方法共$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $种
15.某市植物园要在30天内接待20所学校的学生参观,但每天只能安排一所学校,其中有一所学校人数较多,要安排连续参观2天,其余只参观一天,则植物园30天内不同的安排方法有$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $。
16.某校准备组建一个由12人组成篮球队,这12个人由8个班的学生组成,每班至少一人,名额分配方案共$\underline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } $种 .
选择题:
1.6个人分乘两辆不同的汽车,每辆车最多坐4人,则不同的乘车方法数为( )
A.40 B.50 C.60 D.70
2.有6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有( )
A.36种 B.48种 C.72种 D.96种
3.只用1,2,3三个数字组成一个四位数,规定这三个数必须同时使用,且同一数字不能相邻出现,这样的四位数有( )
A.6个 B.9个 C.18个 D.36个
4.男女学生共有8人,从男生中选取2人,从女生中选取1人,共有30种不同的选法,其中女生有( )
A.2人或3人 B.3人或4人 C.3人 D.4人
5.某幢楼从二楼到三楼的楼梯共10级,上楼可以一步上一级,也可以一步上两级,若规定从二楼到三楼用8步走完,则方法有( )
A.45种 B.36种 C.28种 D.25种
6.某公司招聘来8名员工,平均分配给下属的甲、乙两个部门,其中两名英语翻译人员不能分在同一个部门,另外三名电脑编程人员也不能全分在同一个部门,则不同的分配方案共有( )
A.24种 B.36种 C.38种 D.108种
7.已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为( )
A.33 B.34 C.35 D.36
8.由1、2、3、4、5、6组成没有重复数字且1、3都不与5相邻的六位偶数的个数是( )
A.72 B.96 C.108 D.144
9.如果在一周内(周一至周日)安排三所学校的学生参观某展览馆,每天最多只安排一所学校,要求甲学校连续参观两天,其余学校均只参观一天,那么不同的安排方法有( )
A.50种 B.60种 C.120种 D.210种
10.将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有
(A)12种 (B)18种 (C)36种 (D)54种
11.某单位安排7位员工在10月1日至7日值班,每天1人,每人值班1天,若7位员工中的甲、乙排在相邻两天,丙不排在10月1日,丁不排在10月7日,则不同的安排方案共有
A. 504种 B. 960种 C. 1008种 D.1108种
提交方法
提交cpp文件,用puts()输出每一个答案,如有不会的题,要输出一个空行。
